האלגוריתם Quicksort ותהליך החלוקה

Quicksort הוא אלגוריתם יעיל במיוחד לסידור פריטים.

Quicksort מבוסס על גישת "הפרד ומשול" Divide and conquer שמפצלת בעיה גדולה לבעיות משנה שקל יותר לפתור. אם בעיות המשנה הם לא מספיק קלות לפתרון מפצלים גם אותם. וחוזר חלילה עד שמגיעים לבעיות שקל לפתור. האלגוריתם פותר את בעיות המשנה שקל לפתור, וממזג את הפתרונות חזרה לפתרון הבעיה הגדולה.

Quicksort מסדר פריטי מערך על ידי:

1. חלוקות המערך לשני חלקים. כך שחלק אחד מכיל את הפריטים הגדולים ושני את הפריטים הקטנים.
2. Quicksort קורא לעצמו באופן רקורסיבי במטרה לסדר את שני חלקי המערך.
3. אחרי סידור תתי המערכים, מחבר את שני חלקי המערך המסודרים למערך גדול יותר.

הסידור הוא inline ולכן אנחנו תמיד עובדים בתוך אותו מערך בכל פעם על חלק אחר שלו. לכן, כשקוראים ל-Quicksort חשוב להגדיר על איזה חלק של המערך הוא צריך לעבוד. את זה עושים על ידי שימוש באינדקסים, l משמאל ו-r מימין.

נניח מערך A אותו נעביר ל-Quicksort למיון תוך שאנו מגדירים את גבולות החלק של המערך אותו יש למיין על ידי הגדרת האינדקסים l ו-r:

Quicksort(A[l, r])

אם המערך מכיל יותר מפריט אחד אז האינדקס משמאל, l, קטן מאשר האינדקס מימין, r, אז נפעיל עליו פונקציה Partition שתפקידה לפצל את המערך סביב הציר Pivot לשניים, פריטים גדולים מימין וקטנים משמאל, להביא את הציר למקומו הנכון במערך, ולהחזיר את מיקום הציר בתור האינדקס p עליו יש לפצל:

Quicksort(A[l, r]):
    if l < r:
        p = Partition(A[l, r])

אחרי שאנחנו יודעים על מה לפצל נקרא ל-Quicksort על החלק של המערך הקטן מ-p:

Quicksort(A[l, p-1])

ועל חלקו של המערך הגדול מ-p:

Quicksort(A[p+1, r])

הקריאה ל-Quicksort נעשית באופן רקורסיבי כאשר הפונקציה קוראת לעצמה:

Quicksort(A[l, r]):
    if l < r:
        p = Partition(A[l, r])
        Quicksort(A[l, p-1])
        Quicksort(A[p+1, r])

לכל רקורסיה צריך להיות מקרה בסיס. משהו שעוצר אותה מלהמשיך לנצח (או עד לקריסת התוכנה). במקרה של Quicksort מקרה הבסיס הוא כאשר המערך הוא באורך של פריט 1 או פחות. זאת אומרת, כל עוד l קטן מ-r.

לסיכום, Quicksort מפצל את המערך אותו צריך לסדר לשני חלקים סביב ציר Pivot שאותו בוחר תהליך הפיצול Partition. בחלק אחד נמצאים הפריטים הקטנים. בחלק שני נמצאים הפריטים הגדולים.

תהליך החלוקה Partition

החלק המעניין באמת באלגוריתם Quicksort שגם עושה את רוב העבודה הוא תהליך החלוקה Partition. במסגרת תהליך החלוקה בוחרים ציר Pivot כאשר האלגוריתם מסדר את המערך כך שכל מה שלשמאלו של הציר קטן יותר ומה שמימין גדול יותר.

נניח שהפונקציה שעושה Partition מקבלת את המערך הבא:

A = [5 3 1 4 2]

אם הציר Pivot שהפונקציה בוחרת יהיה, לדוגמה, 3 אז האלגוריתם יגרום לזה שכל מה שמשמאל לציר יהיה קטן יותר מ-3 ומה שמימין גדול יותר.

פלט אפשרי:

A = [2 1 3 4 5]

פלט נוסף אפשרי:

A = [2 1 3 5 4]

זה לא מחייב שהאגף הימני והשמאלי יהיו מסודרים בסדר עולה. רק שאגף שמאל ירכז את הערכים הקטנים יותר מ-Pivot וימין את הערכים הגבוהים יותר.

לתהליך החלוקה Partition יש 2 מטרות:

1. להביא את הצירPivot למקום הנכון במערך. כאשר מימין לו הערכים הגבוהים ממנו, ומשמאל הערכים הנמוכים.
2. להחזיר את האינדקס בו נמצא הציר Pivot כאשר הפונקציה מסיימת . זה חשוב כי זה מה שמאפשר ל- Quicksort לדעת מהם חלקי המערך שצריך עוד לסדר.

def quicksor(A[l, r]):
    if l < r:
        p = partition(A[l, r])
        quicksort(A[l, p-1])
        quicksort(A[p+1, r])

קיימות דרכים שונות לחלק את המערך. במדריך זה נעשה partition על פי Hoare הנקרא על שמו של המדען שהמציא את האלגוריתם Quicksort.

במהלך החלוקה צריך להבחין בין 2 דברים: מיקום הציר Pivot לעומת הערך של Pivot. המיקום, האינדקס של Pivot עשוי להשתנות בתהליך החלוקה Partition אולם הערך של הציר Pivot נשאר קבוע.

נסביר את השלבים של תהליך החלוקה Partition על פי אלגוריתם Hoare:

1. בחירת הציר Pivot. קיימות גישות שונות לבחירת הציר, כפי שנראה בהמשך. בשביל הפשטות נבחר את הפריט הראשון של המערך בתור הציר.
2. כאשר המטרה היא להביא את הציר Pivot למקום הנכון במערך.

קלט לדוגמה:

A = [2 1 4 5 3]

פלט לדוגמה:

A = [1 2 4 5 3]

• הערכים בפלט לא מסודרים בהכרח לפי הסדר הנכון אבל הערכים מימין לציר הם גדולים יותר ממנו והערכים משמאל קטנים יותר.

נגדיר שני מצביעים cursors להם נקרא i ו-j שיקיימו:

• כיוון שהציר Pivot נמצא בעמדה השמאלית ביותר l, אז המצביע i ימצא בעמדה הבאה אחריו.
• המצביע j ימצא בעמדה הימנית ביותר שסימנה r.

p = A[l]  // leftmost index
i = l + 1 // 1 position to the right of the pivot
j = r // rightmost index

• המצביע i יתקדם בכל פעם במקום 1 כשהוא נע משמאל לימין i += 1
• המצביע j ירד בכל פעם באינדקס 1 כשהוא נע מימין לשמאל j -= 1

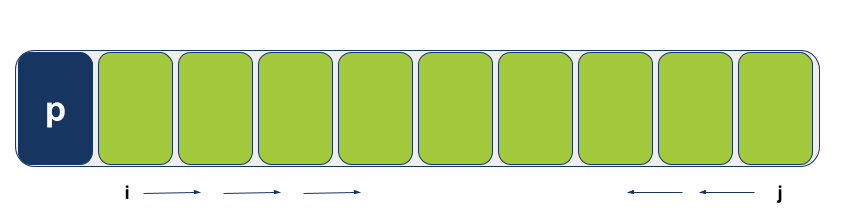
המצביעים לא רק נעים הם גם עוצרים בתנאים מסוימים.

• המצביע i ימשיך לנוע משמאל לימין עד שהוא יעצר על אלמנט שהערך שלו גדול או שווה לערך הציר Pivot:

  A[i] >= p

• המצביע j ימשיך לנוע מימין לשמאל עד שהוא ייעצר על אלמנט שהערך שלו קטן או שווה לציר:

  A[j] <= p

המצביע i ינוע עד שהוא ייעצר על אלמנט גדול או שווה לציר Pivot מה שאומר שכל מה שנמצא משמאלו ועד לציר הוא קטן יותר מאשר ערך הציר:

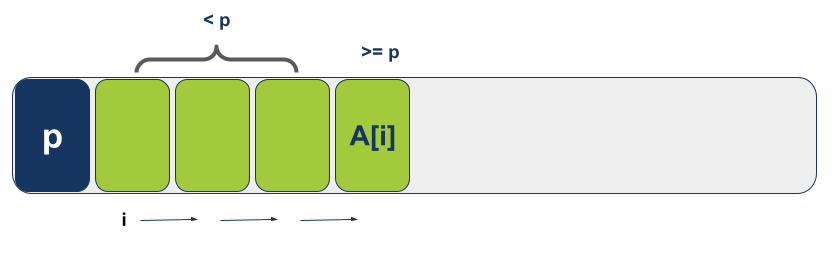
המצביע j ינוע עד שייעצר על אלמנט קטן או שווה לציר Pivot מה שאומר שכל מה שנמצא לימינו הוא גדול יותר מערך הציר.

אחרי ששני המצביעים i ו-j נעצרו נבחין בין שני מצבים:

1. מצב ראשון בו המיקום של j גדול מ-i

   

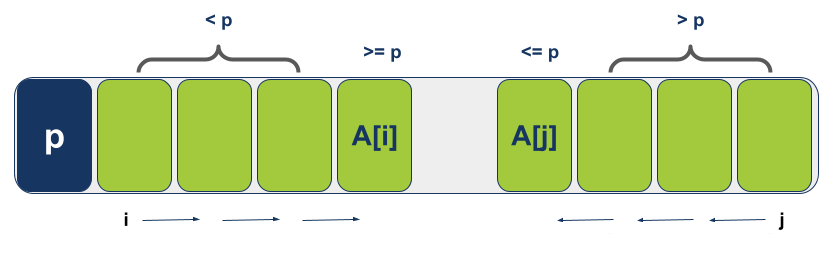
   • ערך האלמנט עליו מצביע j קטן או שווה מערך הציר Pivot, וכל מה שנמצא לימינו גדול מערך הציר.
   • ערך האלמנט עליו מצביע i גדול או שווה מערך הציר Pivot וכל מה שנמצא לשמאלו קטן מערך הציר Pivot.

   יוצא שהמקומות עליהם מצביעים i ו-j שוברים את הרצף אז נחליף ביניהם swap כדי לקיים את הסדר בו כל מה שנמצא ימינה מ-j הוא גדול או שווה לערך הציר Pivot, ומה שנמצא משמאל לi הוא קטן או שווה לערך הציר.

   אחרי ההחלפה בין הערכים של המצביעים, יש להמשיך את התנועה של i ו-j מהמקום בו נעצר התהליך לצורך החלפה.

2. מצב שני בו המצביעים i ו-j חוצים אחד את השני.

   זה מצב בו המיקום (=האינדקס) של המצביע j הוא קטן או שווה ל-i.

   

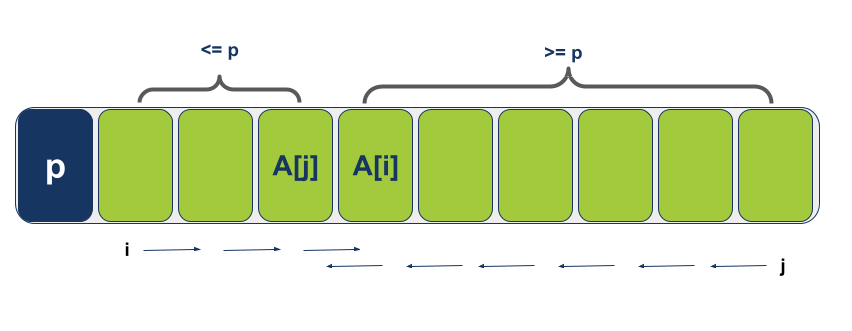
   • כל מה שמימין ל-i כולל i הוא גדול (או שווה) מערך הציר Pivot
   • כל מה שמשמאל ל-j כולל j הוא קטן (או שווה) מערך הציר

   זאת אומרת שהאגפים מסודרים עכשיו. אגף ימין מרכז את הערכים הגדולים ואגף שמאל את הקטנים:

   

   הדבר היחיד שאינו במקומו הוא הציר Pivot, שצריך להיות בין המצביעים i ו-j, אז מה שמתבקש לעשות הוא לשים את הציר במקומו. לשם כך, נחליף את המקומות בין ערך הציר לבין הערך עליו מצביע j.

אחרי ש-Partition מיקם את הציר במקומו הנכון והסופי במערך הכולל, הוא יחזיר את מיקום (=אינדקס) הציר ל-Quicksort כדי שיפצל עליו את המערך לשני תתי מערכים אשר יועברו אף הם באופן רקורסיבי ל-Quicksort להמשך מיון.

 

איך עובד Quicksort - בסבלנות שלב אחר שלב

נעביר לפונקציה Quicksort את המערך הבא כדי שתסדר אותו בסדר עולה:



כיוון שהמערך ארוך מספיק (מכיל יותר מפריט אחד) הפונקציה Quicksort תעביר אותו לפונקציה Partition.

הפונקציה Partition:

1. תקבע ציר Pivot אותו היא תביא למיקום הנכון במערך.
2. תסדר את המערך: פריטים גדולים מימין לציר Pivot וקטנים משמאל.
3. תחזיר ל-Quicksort את העמדה של הציר סביבה צריך לחצות את המערך.

בהסבר שלנו נאפשר ל-Partition למקם את הציר באופן פשוט על ידי כך שהיא תגדיר תמיד את הפריט השמאלי ביותר של המערך בתור הצירPivot. המצביע i יוצב מימין לציר, המצביע j יוצב בעמדה הימנית ביותר של המערך:



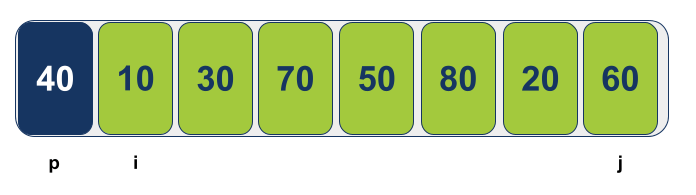
המצביע i יתקדם משמאל לימין עד למציאת ערך גדול (או שווה) לערך הציר:



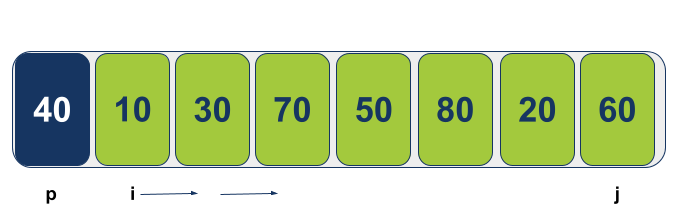
המצביע j יתקדם מימין לשמאל עד למציאת ערך קטן (או שווה) מערך הציר:



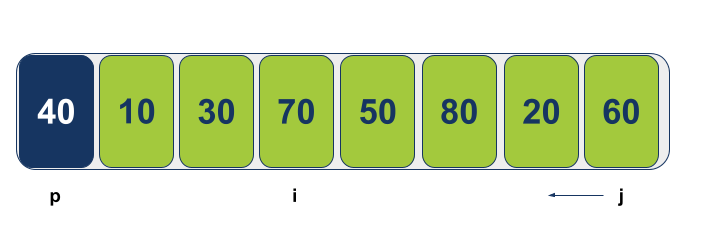
אחרי שהמצביעים i ו-j מגיעים למקומם ועוצרים, אנחנו רואים שהם לא חצו אחד את השני.

אנחנו רואים:

• שכל מה שמימין למצביע j הוא גדול מערך הציר אבל הערך עליו עומד המצביע j הוא קטן (או שווה) לציר.
• וכל מה שמשמאל למצביע i הוא קטן מערך הציר, אבל המצביע i הוא גדול (או שווה) לערך הציר.

כלומר, מה שלא נמצא במקומו, מה ששובר את הרצף, הוא היכן שהמצביעים עומדים. בהתאם, מתבקש שנחליף בין הערכים עליהם מצביעים המצביעים כדי שכל מה שגדול (או שווה) מהציר יהיה מימין וכל מה שקטן (או שווה) יהיה משמאל. אם כך, אז נחליף בין הערכים:



• מחליפים את הערכים עליהם עומדים המצביעים אך לא את המקומות.

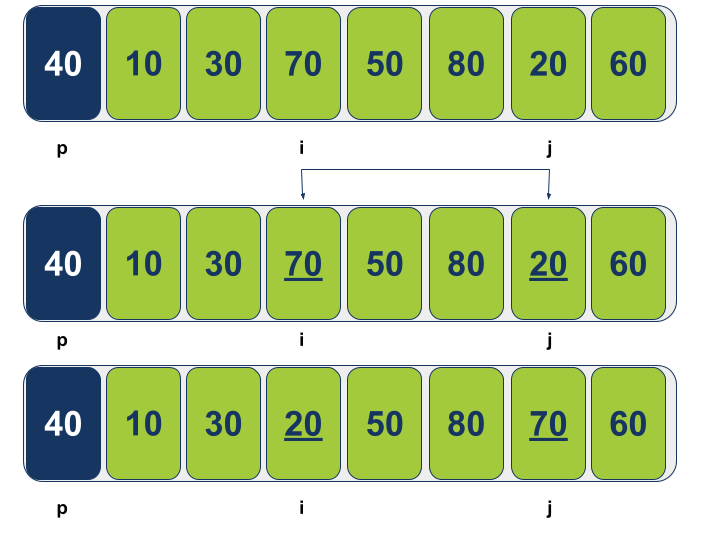
אומנם החלפנו אבל הפונקציה לא סיימה. המצביעים i ו-j צריכים להמשיך ולהתקדם עד שדרכיהם מצטלבות.

נמשיך את התנועה של המצביע i ימינה כדי לחפש ערך גדול או שווה לציר, ואת התנועה של המצביע j לשמאל במטרה למצוא ערך קטן או שווה לציר. כשהמצביעים מוצאים ערכים שעונים על הדרישות הם עוצרים בהם:



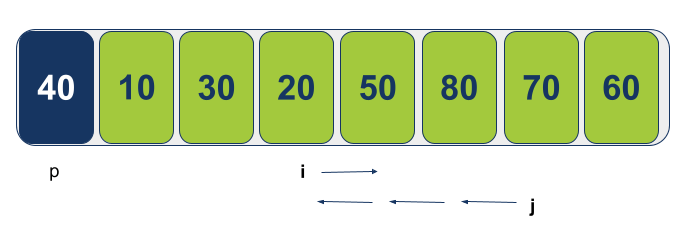
הפעם, המצביעים i ו-j חצו אחד את השני:



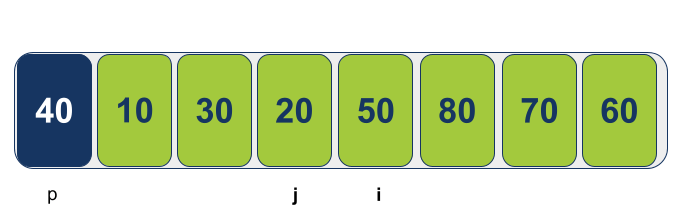
עכשיו כשהמצביעים חצו אחד את השני אפשר לראות שכל מה שמימין ל-j הוא גדול (או שווה) לציר, וכל מה שמשמאל ל-j הוא קטן או שווה לציר. לפיכך, הדבר המתבקש הוא להעביר את הציר למקומו הנכון היכן שנמצא j. בהתאם, נחליף את הערך בעמדת הציר עם הערך בעמדה עליה מצביע j:



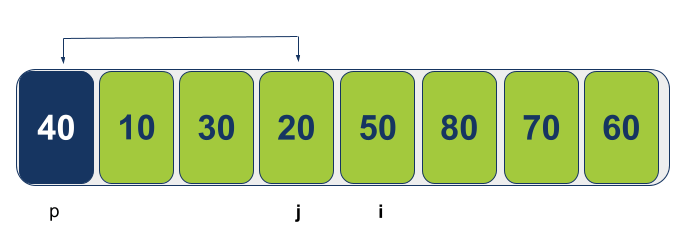
אחרי ההחלפה j מצביע על הציר-pivot שעכשיו נמצא במקומו הנכון:



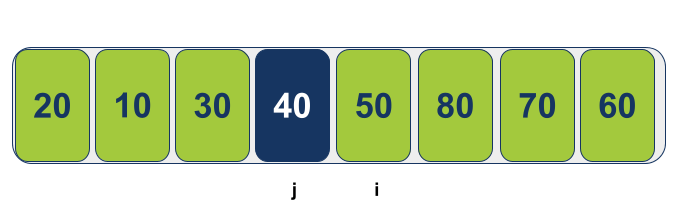
הפונקציה Partition מחזירה את המיקום עליו מצביע j ל-Quicksort בתור העמדה שסביבה צריך לחצות את המערך וגם בתור אלמנט שנמצא עכשיו במקומו הנכון במערך:



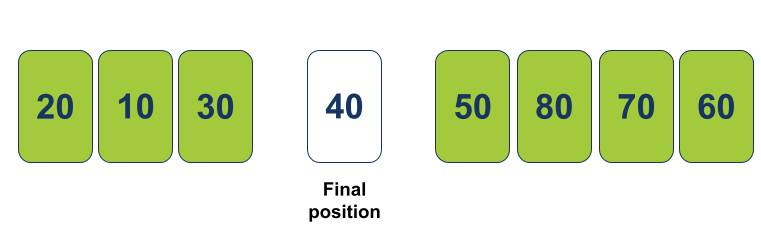
אומנם הצלחנו למקם פריט אחד במקומו הנכון אבל תהליך המיון Quicksort רחוק מסיום.

נעביר לפונקציה Quicksort את חלקו השמאלי של המערך באופן רקורסיבי (הפונקציה קוראת לעצמה):



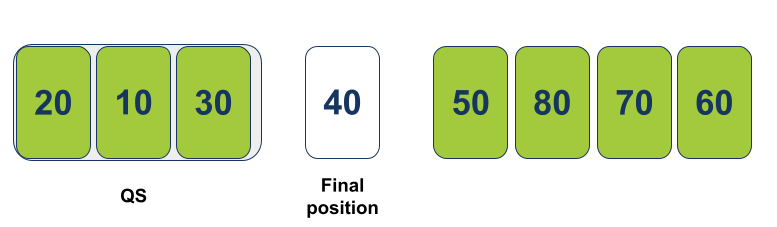
כיוון שתת המערך השמאלי אותו העברנו לפונקציה למיון ארוך מספיק (מכיל יותר מפריט אחד) הפונקציה Quicksort תעביר אותו לפונקציה Partition כדי שתסדר אותו סביב הציר Pivot כך שהערכים הגדולים מימין לציר והערכים הקטנים משמאל, וגם תחזיר את המיקום הנכון של הערך בתור העמדה סביבה צריך לחצות את המערך:



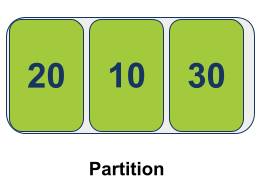
הפונקציה Partition מגדירה את העמדה השמאלית ביותר בתור הציר Pivot ומציבה את המצביעים i משמאל ו-j מימין:



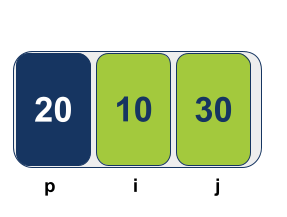
המצביע i מתקדם משמאל לימין במטרה למצוא ערך הגדול (או שווה) לערך הצירPivot. המצביע j מתקדם מימין לשמאל במטרה למצוא ערך הקטן (או שווה) מערך הציר.



• המצביעים מצאו ערכים המקיימים את התנאים, ולכן עצרו.
• אנחנו רואים שהצטלבו דרכי המצביעים i ו-j.

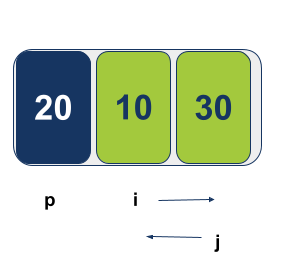
כיוון שמצביע i עצר בעמדה גבוהה מהעמדה בה עצר המצביע j, הפונקציה תחליף swap בין הערך בעמדת הציר לבין הערך עליו מצביע j:



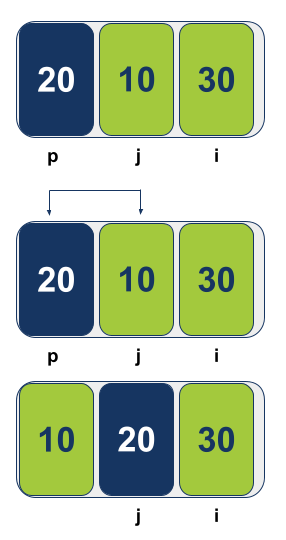
לאחר ההחלפה הצירPivot נמצא במקומו הנכון במערך. העמדה בה נמצא ערך הציר היא העמדה עליה מצביע j.

הפונקציה Partition תחזיר ל-Quicksort את האינדקס של j כאשר מה שמימין לציר גדול יותר ומה שמשמאל קטן יותר.



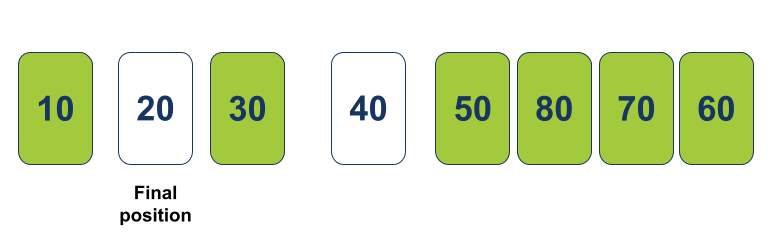
Quicksort יקרא לעצמו באופן רקורסיבי כדי לטפל בצידו השמאלי של המערך לאחר החלוקה:



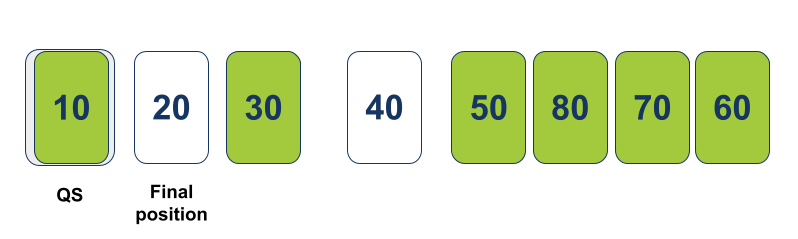
כיוון שאורך המערך אותו קיבלה הפונקציה Quicksort הוא 1, הרקורסיה עוצרת, ומוחזר המערך כמות שהוא. המערך המוחזר מכיל פריט 1 שנמצא במקומו הנכון במערך הכולל:



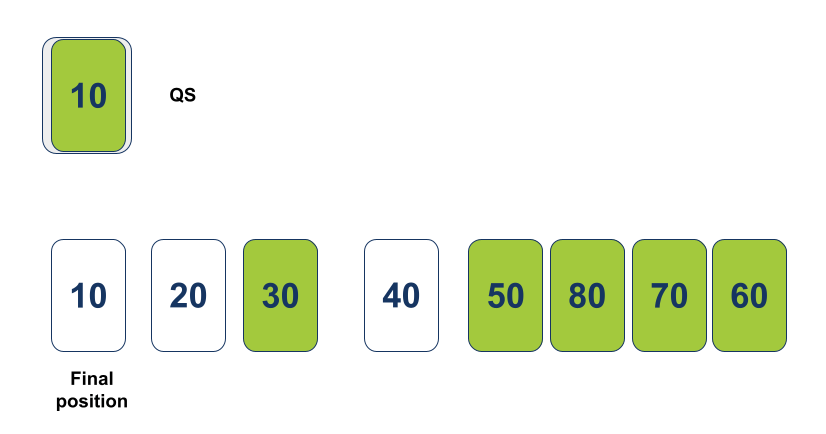
Quicksort יקרא לעצמו באופן רקורסיבי כדי לטפל בצידו הימני של המערך שחולק:



• אורך המערך אותו קיבלה Quicksort היה 1 מה שגרם לעצירת הרקורסיה, והחזרת המערך המכיל פריט בודד שנמצא במקומו הנכון במערך הכולל.

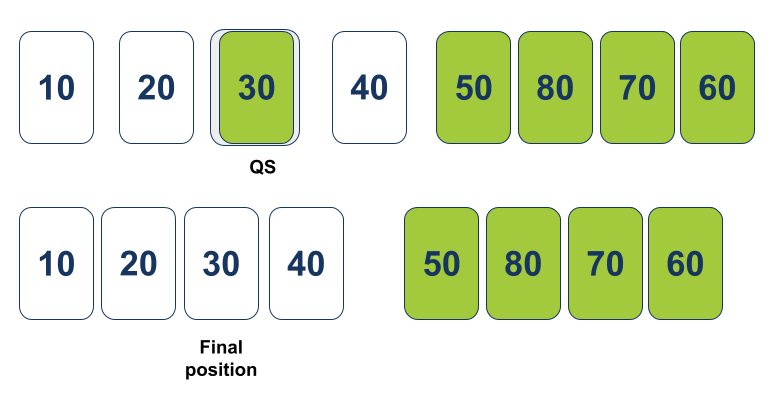
עכשיו Quicksort עובר לטפל בחלקו הימני של המערך כפי שהוגדר בעקבות הקריאה הראשונה לתהליך החלוקה Partition. אחרי ש-Quicksort יקרא לעצמו על המערך הימני הוא יעביר אותו לפונקציה Partition שתציב את הציר Pivot ואת המצביעים i ו-j:



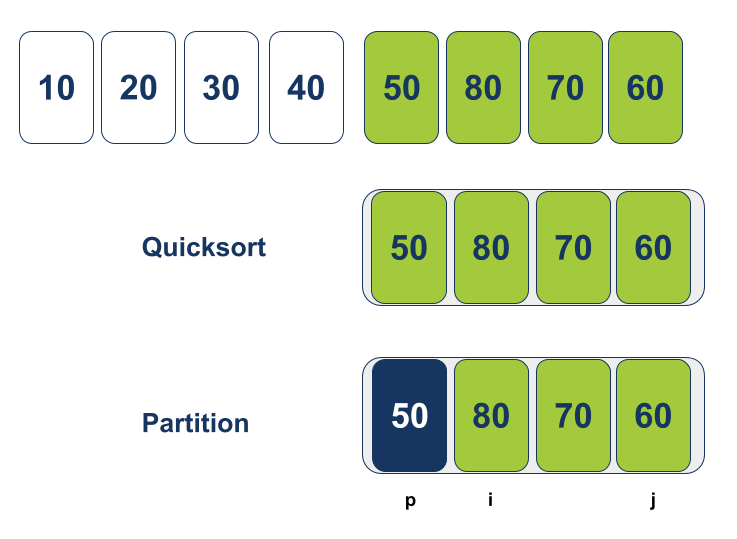
המצביע i אמור לנוע ימינה כדי למצוא ערך גבוה (או שווה) לערך הציר Pivot. המצביע j צריך לנוע שמאלה במטרה למצוא ערך נמוך (או שווה):



• כיוון ש- i מצביע על ערך הגבוה מערך הציר לא היה צורך לקדם אותו.
• המצביע j נדד 3 מקומות עד שהגיע לערך הנמוך או שווה לערך הציר שהוא במקרה זה הציר עצמו.

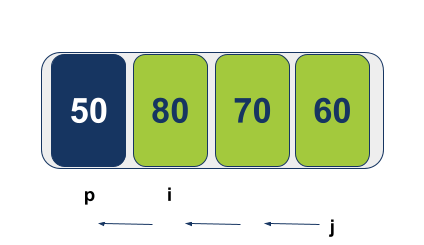
בסך הכל קיבלנו הצטלבות של הסמנים i ו-j; מה שמימין ל-j גדול או שווה. אבל אין משהו משמאל.



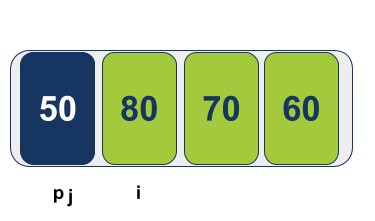
המסקנה היא שהציר נמצא במקומו הנכון, ולכן אין צורך בהחלפה. נחזיר את הערך עליו מצביע j. האלגוריתם עכשיו יכול להבטיח לנו שערך הציר Pivot נמצא במקומו הנכון:



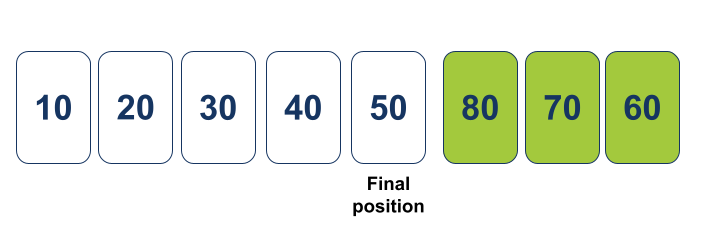
פונקציית ה-Partition החזירה ל-Quicksort מערך ימני בלבד שעדיין צריך לסדר. הפונקציה Quicksort מעבירה ל-Partition את תת המערך הימני כדי שיסדר אותו ויחזיר את מיקום הציר-Pivot עליו צריך לחצות את המערך:



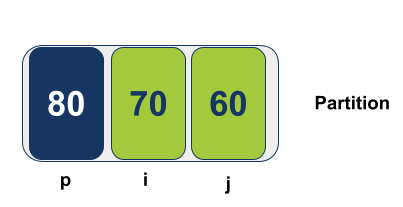
אחרי הצבת הציר Pivot והמצביעים i משמאל ו-j מימין, המצביע i יוצא למסעו לימין במטרה למצוא ערך הגבוה (או שווה) מערך הציר. לשם כך הוא מתקדם בעמדה 1. j מחפש ערך הנמוך או שווה מערך הציר. כיוון שהוא מצביע כבר על ערך הנמוך מערך הציר אין צורך שיזוז ועל כן הוא יישאר במקומו.



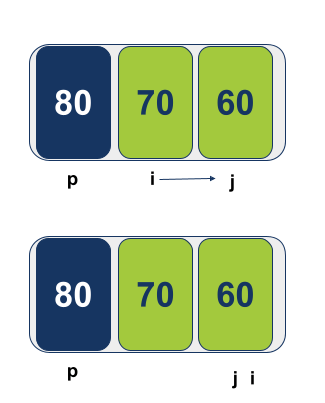
מכיוון ש-i ו-j חצו אחד את השני נחליף בין הערכים במיקום עליו מצביע j והערך של Pivot:



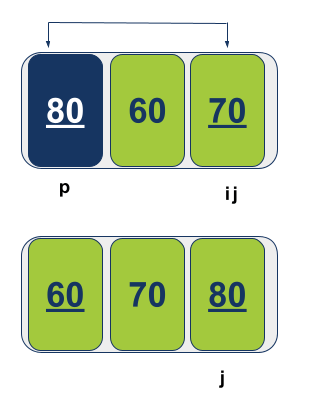
עכשיו אנחנו יודעים שהציר נמצא במקומו הנכון במערך הכולל:



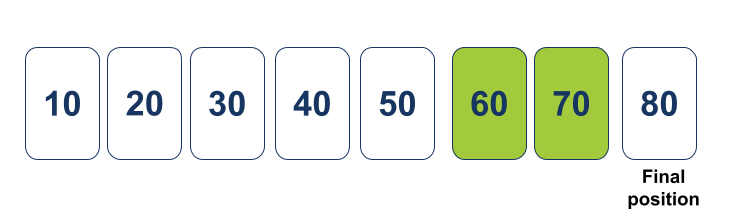
נחזיר את המערך המסודר ל-Quicksort כדי שיעביר ל-Partition את תת המערך השמאלי לצורך סידור:



• אחרי הצבת הציר Pivot במערך שיש בו רק 2 מקומות. לא נשאר אלא למקם את שני המצביעים על הפריט הנוסף במערך.

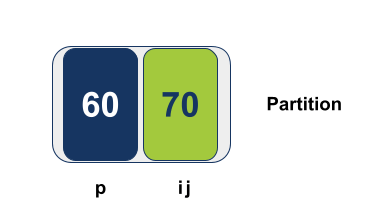
המצביע i אמור להתקדם ימינה אבל אין לו לאן. לכן ישאר במקומו. המצביע j מתקדם שמאלה צעד אחד במטרה למצוא ערך הקטן או שווה לערך הציר Pivot:



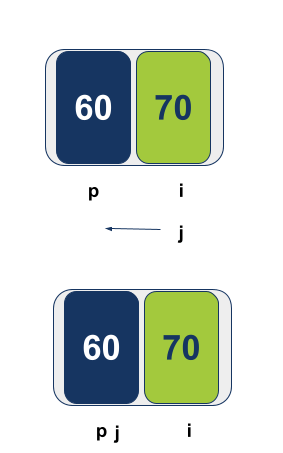
הפונקציה Partition מחזירה ל-Quicksort את הציר שעכשיו אנחנו יודעים בביטחון שנמצא במקומו הנכון, בנוסף למערך שיש בו פריט אחד בלבד מימין לציר:



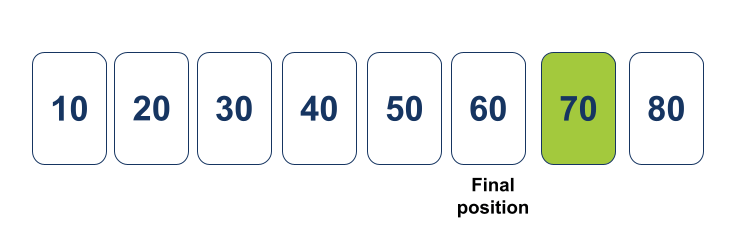
הפונקציה Quicksort קראה לעצמה באופן רקורסיבי על מערך המכיל פריט בודד מה שגרם להפעלת התנאי המפסיק את הרקורסיה. כתוצאה מכך חוזר המערך כמות שהוא ועכשיו אנחנו יכולים לדעת בוודאות שהערך היחיד שנמצא בתוך המערך אכן נמצא במקומו הנכון במערך הכולל:



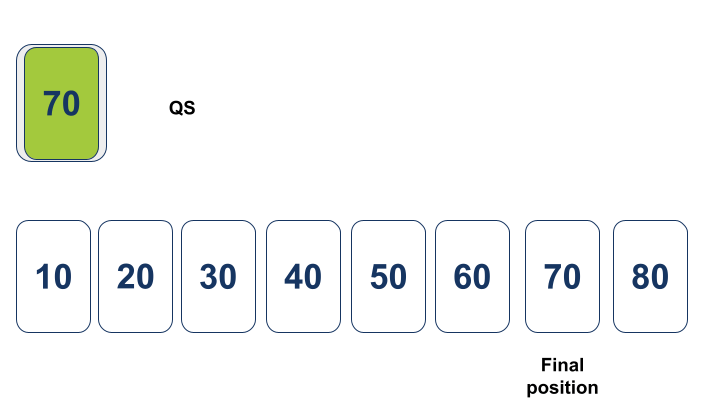
אין אפשרות יותר לקרוא ל-Quicksort כי אין יותר מערכים שאותם צריך לסדר, ולכן Quicksort סיים. המערך הכולל מסודר עכשיו:



 

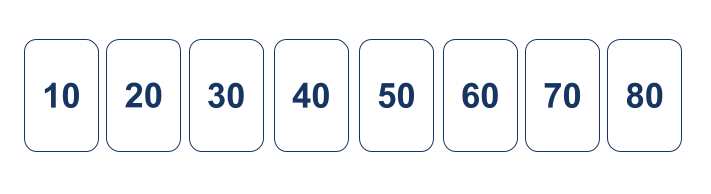
קוד פייתון לביצוע Quicksort

אחרי שהסברנו כיצד עובד Quicksort נראה את הקוד לסידור פריטי מערך תוך שימוש ב-Hoare Partition.

הפונקציה quicksort עובדת על המערך הכולל ועל תתי המערכים שלו. כדי לדעת על איזה חלק של המערך היא צריכה לעבוד היא מקבלת בתור פרמטרים את המערך הכולל ואת האינדקסים התוחמים את תת המערך. היא מעבירה את תת המערך לתהליך החלוקה Partition אשר חוצה את המערך סביב ציר Pivot. התוצאה של החלוקה היא ערך שנמצא במיקום האינדקס הנכון שלו כאשר מה שמימין לו במערך קטן יותר ומה שמשמאל גדול. על שני החלקים, הימני והשמאלי, הפונקציה quicksort קוראת לעצמה באופן רקורסיבי. תנאי הבסיס להפסקת הרקורסיה, המקרה הטריוויאלי, הוא כאשר אורך תת המערך לסידור הוא פריט 1. במקרה זה הפונקציה עוצרת, והיא יכולה להבטיח לנו שהפריט בתת המערך נמצא במקומו הנכון והסופי במערך הכולל.

# sorts a (portion of an) array,
# divides it into partitions, then sorts those
def quicksort(arr, lo, hi):
   # the base case that ends the recursion
   # is when the subarray
   # has less than 1 element
   if lo < hi:
       # the partition puts the pivot element
       # in its final position in the array such that
       # every item to its left is smaller
       # and every item to its right is larger
       p = partition(arr, lo, hi)
      
       # recursive call on the left subarray
       quicksort(arr, lo, p-1)
      
       # recursive call on the right subarray
       quicksort(arr, p+1, hi)

הפונקציה partition אחראית על תהליך החלוקה. מטרת החלוקה:

1. להביא את הציר Pivot למקום הנכון במערך. כאשר מימין לו הערכים הגבוהים ממנו, ומשמאל הערכים הנמוכים.
2. להחזיר את האינדקס בו נמצא הציר Pivot כאשר הפונקציה מסיימת . זה חשוב כי זה מה שמאפשר ל- Quicksort לדעת מהם חלקי המערך שצריך עוד לסדר.

# returns the partition index
# for subarray between indices l and r
def partition(arr, lo, hi):
   # choose Pivot to be the first subarray element
   p_index = lo
   pivot = arr[p_index]


   # left cursor
   i = lo + 1
  
   # right cursor
   j = hi
  
   # loop as long as the cursors don't cross
   while True:
       # move the i cursor to the right
       # as long as its value is less than 
       # the value of the pivot
       while i < hi:
           if arr[i] >= pivot:
               break
           else:
               i += 1
          
       # move the j cursor to the left
       # as long as its value is greater 
       # than the value of the pivot
       while j > lo:
           if arr[j] <= pivot:
               break
           else:
               j -= 1
          
       # if the cursors cross
       # swap the values that j points to
       # with the pivot value
       # and return j's position.
       # Now the pivot's value is
       # at its final position in the 
       # overall array
       if i >= j:
           swap(arr, p_index, j)
           return j
      
       # if the cursors don't cross
       # swap the values that
       # i and j point to
       # but don't return since i
       # and j need to continue in
       # their journey until they cross
       swap(arr, i, j)

הפונקציה partition משתמשת בפונקציה swap בשביל להחליף בין פריטים במערך:

# swap
def swap(arr, i, j):
   if i != j:
       tmp = arr[i]
       arr[i] = arr[j]
       arr[j] = tmp
   return arr

אפשר לעשות החלפה באמצעות תחביר מקוצר בפייתון:

arr[i], arr[j] = arr[j], arr[i]

• אבל זה תחביר של פייתון והמטרה שלי במדריך היא לפתח קוד שניתן לתרגם אותו בקלות לשפות מחשב נוספות.

נבדוק שהקוד עובד עבור כל מיני מצבים. מערך ריק, חזרות על אלמנטים במערך, מערך מסודר בסדר נכון, מערך מסודר בסדר הפוך, וכיו"ב:

tests = [
   [40, 10, 30, 70, 50, 80, 20, 60,],
   [],
   [10, 20, 30, 40, 50, 60, 70, 80,],
   [80, 70, 60, 50, 40, 30, 20, 10,],
   [-80, 20, 202, -80, 33],
   [4, 2, 0, 42, 2, -1, 3, 5, 28]
]


for arr in tests:
   quicksort(arr, 0, len(arr)-1)
   print(f"sorted array: {arr}")

התוצאה:

sorted array: [10, 20, 30, 40, 50, 60, 70, 80]
sorted array: []
sorted array: [10, 20, 30, 40, 50, 60, 70, 80]
sorted array: [10, 20, 30, 40, 50, 60, 70, 80]
sorted array: [-80, -80, 20, 33, 202]
sorted array: [-1, 0, 2, 2, 3, 4, 5, 28, 42]

 

הערכת ביצועי האלגוריתם Quicksort

כדי להבין את הקומפלקסיות של האלגוריתם Quicksort צריך להבין שהוא עובד בשני חלקים: תהליך החלוקה Partition ורקורסיה. נעריך את הקומפלקסיות של כל חלק, ואז נשלב בין ההערכות כדי לקבל אומדן על ביצועי האלגוריתם בסך הכל.

כשעושים Hoare Partition המצביעים מתקדמים בכל פעם במיקום 1, כאשר העבודה היא החלפה swap. המקרה הגרוע ביותר הוא שכל פעם שהמצביעים מתקדמים מתבצעת החלפה: מצביע i מתקדם מקום 1 ועוצר, מצביע j מתקדם 1 ועוצר, ואז החלפה. וחוזר חלילה עד שמגיעים לסוף המערך. זה המקרה הגרוע ביותר. באופן מעשי, המצביע j לא יכול להתקדם יותר מצעד 1 מעבר למיקום של i אבל את זה נזניח כשאנו מעריכים את ביצועי האלגוריתם. המסקנה היא, שאם גודל המערך הוא n אז המצביע i יכול להתקדם לכל היותר n מקומות וגם המצביע j יכול להתקדם לכל היותר n מקומות. בסה"כ לכל היותר 2n החלפות swaps מה שנותן לנו משך זמן לינארי גם עבור המקרה הגרוע ביותר של ביצוע תהליך החלוקה. לפיכך, תהליך החלוקה Partition מציג קשר לינארי בין התארכות הקלט ומשך הזמן לביצוע:

O(N)

כדי להעריך את הקומפלקסיות של הרקורסיה נבחין בין שני מצבים. המקרה הטוב ביותר והגרוע:

במקרה הטוב תהליך החלוקה מחלק את המערך בכל פעם לשני חלקים שווים מה שגורם לקומפלקסיות לוגריתמית של הרקורסיה:

O(LogN)

במקרה הגרוע החלוקה היא הכי לא שווה שיכולה להיות, כמו המצב שבו הקלט הוא מערך מסודר, בסדר נכון או בסדר הפוך, אז בכל פעם החלוקה מחלקת פריט אחד מתוך המערך ומקצרת את אורכו של המערך הלא מסודר במקום 1. במקרה כזה הקומפלקסיות היא לינארית:

O(N)

אחרי שיש לנו הערכה של משך הביצוע עבור תהליך החלוקה Partition ועבור הרקורסיה נשלב ביניהם לצורך הערכת ביצועי האלגוריתם Quicksort.

קומפלקסיות הזמן עבור משך הביצוע הקצר ביותר היא מכפלה של המקרה הטוב ביותר מבחינת הרקורסיה בעבודה שמבצע התהליך Partition. בהתאם, עבור מערך באורך N פריטים, נכפיל את N משך הזמן לביצוע ה-Partition בכל רמה ב- Log N מספר הרקורסיות במקרה שמפצלים את המערך בכל פעם לשני חלקים שווים בדיוק. תוצאת המכפלה היא גידול לינאריתמי של משך זמן הביצוע כתלות בגודל הקלט:

O(N*Log N)

נעזר בעץ רקורסיה כדי להבין את הסיבה לקומפלקסיות הזמן הלינאריתמית. ניקח לדוגמה, מערך של 8 פריטים שבכל רמת רקורסיה מפצלים אותו לשניים:



• אורך המערך הוא 8, ומספר רמות הרקורסיה הוא 3. בהתאם לעובדה שפיצול מערך לשניים בכל רמת רקורסיה מביא ל-Log N רמות רקורסיה כאשר Log 8 = 3.
• בכל אחת מרמות הרקורסיה תהליך החלוקה Partition עובד על ידי ביצוע N החלפות.
• הכפלה של N פעולות (החלפה) אותן מבצע תהליך החלוקה בכל רמה בנפרד במספר הרמות שהוא Log N מביאה לקומפלקסיות זמן לינאריתמית N * Log N

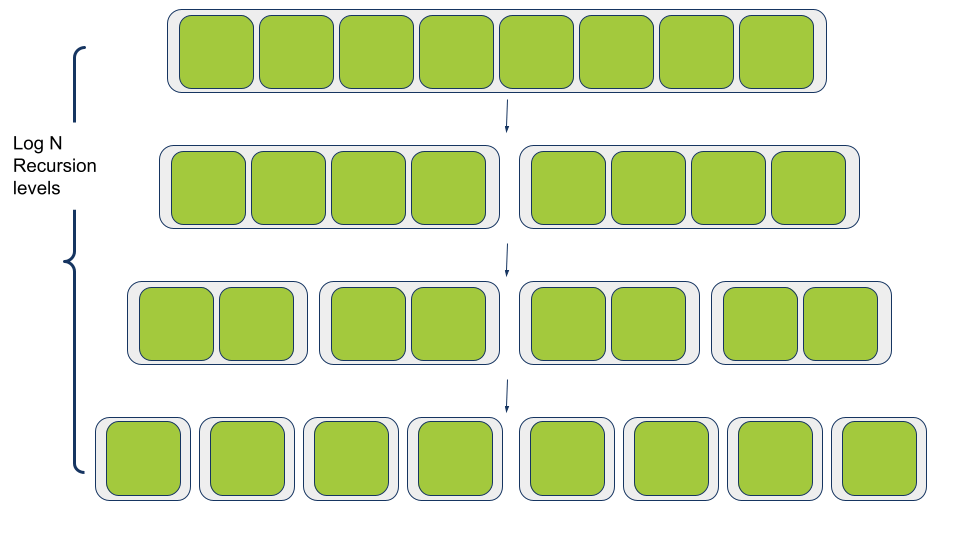
קומפלקסיות זמן במקרה הגרוע ביותר היא מכפלה של המקרה הגרוע ביותר של הרקורסיה בכמות העבודה אותו מבצע תהליך החלוקה בכל רמה:

N X N = N^2

ומכאן גידול פולינומי של משך זמן הביצוע כתלות בגודל הקלט:

O(N^2)

נדגים את המקרה הגרוע ביותר על מערך של 8 פריטים שבכל רמת רקורסיה תהליך החלוקה מפצל ממנו פריט אחד ויחיד:



• אורך המערך הוא N, ומספר רמות הרקורסיה הוא N-1 כי בכל שלב מסירים פריט אחד מהמערך אותו יש לסדר.
• בכל אחת מרמות הרקורסיה תהליך החלוקה Partition עובד על ידי ביצוע N החלפות.
• הכפלה של N החלפות בכל רמה בנפרד ב- N רמות רקורסיה מביאה לקומפלקסיות N^2

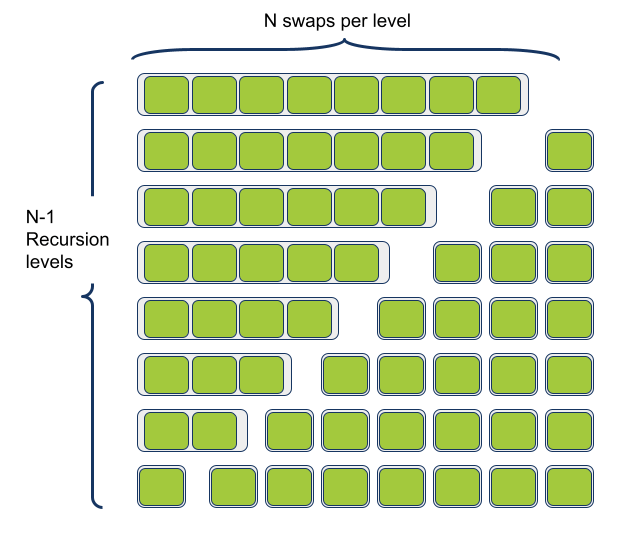
מזה אנחנו יכולים ללמוד שהמקרה הגרוע ביותר עבור קומפלקסיות הזמן הוא כאשר המערך מסודר דבר הגורם לקומפלקסיות זמן פולינומית N^2, והמקרה הטוב ביותר הוא כאשר המערך רנדומלי אז קומפלקסיות הזמן היא לינאריתמית NLogN. בהנחה שמערך רנדומלי הוא המקרה השכיח אז המקרה הממוצע גם הוא בעל קומפלקסיות זמן לינאריתמית NLogN.

אנחנו כמובן רוצים להימנע מביצועים גרועים של האלגוריתם וליהנות מזמן ביצוע קצר כמה שניתן ולכן דרך אחת להפיק מהאלגוריתם ביצועים גבוהים היא באמצעות בחירה אקראית של הציר כי כמו שראינו מערך מסודר מפיק תוצאות גרועות ומערך שסדר הפריטים בו אקראי משיג משך ביצוע מהיר.

לדוגמה, בקוד הבא של הפונקציה partition שיניתי את אופן בחירת הציר Pivot כדי שבמקום שהבחירה תיפול תמיד על הפריט הראשון של המערך הבחירה תהיה אקראית:

# returns the partition index
# for subarray between indices l and r
def partition(arr, lo, hi):
  # choose random index from subarray
  rand_idx = random.randint(lo, hi)
 
  # make the selected index value
  # the first sub-array element
  # by swapping
  swap(arr, rand_idx, lo)
 
  # choose Pivot to be the first sub-array element
  p_index = lo
  pivot = arr[p_index]




  # left cursor
  i = lo + 1
   # right cursor
  j = hi
   # loop as long as the cursors don't cross
  while True:
      # move the left cursor to the right
      # as long as its value is less than
      # pivot
      while i < hi:
          if arr[i] >= pivot:
              break
          else:
              i += 1
        
      # move the right cursor to the left
      # as long as its value is greater
      # than pivot
      while j > lo:
          if arr[j] <= pivot:
              break
          else:
              j -= 1
        
      # if the cursors cross
      # swap the value that j points to
      # with the pivot value
      # and return j's position
      # since the pivot's value is
      # at it's right position
      if i >= j:
          swap(arr, p_index, j)
          return j
    
      # if the cursors don't cross
      # swap the values that
      # that i and j point on
      # don't return since i
      # and j need to continue in
      # their journey
      swap(arr, i, j)

במקרה שמנצלים את כוח האקראיות ביצועי quicksort טובים יותר מ-mergesort. כי למרות ששניהם מפיקים קומפלקסיות זמן לינאריתמית N*LOGN, שנחשבת לגבול עליון הטוב ביותר לביצועי אלגוריתם ממיין, דרישות המקום בזיכרון של quicksort הן נמוכות יותר בגלל שכל העבודה על המערך נעשית בתוך המערך inplace בלי צורך לייצר מערכים נוספים כמו שעושה mergesort.

 

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

אלגוריתם Selection Sort מיון בחירה

אלגוריתם חיפוש בינארי - מהבנה ליישום

big-O ביטוי ליעילות הקוד

 

לכל המדריכים בסדרה ללימוד פייתון

 

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים