מיון טופולוגי באמצעות אלגוריתם Kahn

הבעיה בהבנת מיון טופולוגי topological sort קשורה יותר בשם המפחיד אבל הפעולה של מיון טופולוגי דומה לדברים שאנחנו עושים מדי יום. לדוגמה, שגרת בוקר. קודם צריך לעשות מתיחות או לצחצח שיניים, ואח"כ לפשוט את הפיג'מה ורק אז להכנס למקלחת, אחרי שיוצאים מהמקלחת רק אז כדאי לסרק את השיער, ורצוי לאכול את ארוחת הבוקר רק אחרי צחצוח השיניים, וללכת לעבודה רק אחרי ארוחת הבוקר כי קשה לעבוד על בטן ריקה. סידור של משימות תוך התחשבות בתלויות הוא משהו שאנחנו עושים כל הזמן ובדרך כלל מקדישים לזה יחסית מעט מחשבה. סידור של אובייקטים תוך התחשבות בתלויות היא המהות של מיון טופולוגי.

בתורת הגרפים, מיון טופולוגי או סידור טופולוגי של גרף מכוון הוא סידור לינארי של הצמתים כך שעבור כל קשת מכוונת מצומת B לצומת A כאשר B תלוי ב-A, הסדר יהיה כזה ש- A מקדים את B.

בהינתן רשימת תלויות:

B -> A 
C -> B
D -> C 
E -> D

כאשר B תלוי ב-C, A תלוי ב-D, B תלוי ב-E, C תלוי ב-D. הסדר הטופולוגי צריך להיות:

A -> B -> C -> D -> E

בדוגמה של שגרת הבוקר, הצמתים של הגרף הם המשימות לביצוע, והקשתות מייצגות אילו משימות חייבות להתבצע לפני אחרות כאשר מיון טופולוגי מאפשר יצירת שגרת בוקר עם זרימה נכונה בין המשימות: "לצאת מהמיטה" > "מתיחות" > "צחצוח שיניים" > "להוריד את הפיג'מה" > "מקלחת" > "להתלבש" > "להסתרק" > "לאכול" > "ללכת לעבודה".

מיון טופולוגי אפשרי אם ורק אם הגרף אינו מכיל הפניות מעגליות, כלומר אם הוא גרף מכוון חסר מעגלים (DAG). מיון טופולוגי אפשרי גם כאשר ל-DAG יש רכיבים מנותקים. בנוסף, הוא אינו ייחודי.

בתמונה הבאה אפשר לראות 6 גרפים. נסה לקבוע איזה מהם הינם DAG:

התשובה:

• (1) גרף מכוון (כי יש בו חיצים) וגם אינו מכיל הפניות מעגליות וע"כ הוא DAG.
• (2) אינו מכוון (כי אין בו חיצים) וע"כ אינו DAG.
• (3) גרף מכוון (כי יש בו חיצים) וגם אינו מכיל הפניות מעגליות וע"כ הוא DAG.
• (4) מכיל הפניות מעגליות וע"כ אינו DAG.
• (5) גרף מכוון (כי יש בו חיצים) וגם אינו מכיל הפניות מעגליות וע"כ הוא DAG.
• (6) מכיל הפניות מעגליות וע"כ אינו DAG.

ועוד דבר שצריך להבין לפני שמתחילים הוא שלכל צומת יכולים להיות קשתות שנכנסים אליו ויוצאים ממנו: קשת שמכוונת החוצה מצומת נקראת outbound וקשת שמכוונת אל הצומת נקראת inbound. מזה נגזרות 2 הגדרות נוספות: in-degree של צומת הוא מספר הקשתות המכוונות אליו בעוד out-degree הוא מספר הקשתות המכוונות החוצה מן הצומת.

נביט על הגרף הבא:

• לצומת A יש 2 קשתות המכוונות החוצה ממנו outbound ואין קשתות המכוונות אליו. לפיכך: in-degree = 0 , out-degree = 2

• לצומת C יש 2 קשתות המכוונות אליו inbound ו-0 קשתות המכוונות החוצה ממנו. לפיכך: in-degree = 2 , out-degree = 0

• לצומת B יש קשת 1 המכוונות אליו ו-3 קשתות המכוונות החוצה ממנו, ולפיכך: in-degree = 1 , out-degree = 3

אי אפשר לסדר באמצעות מיון טופולוגי גרף המכיל הפניות מעגליות בגלל שהמטרה של מיון טופולוגי היא לסדר אובייקטים באופן ליניארי: אובייקט אחר אובייקט, משימה B אחר משימה A שבה היא תלויה, ואם משימה אחת תלויה בשנייה שתלויה בראשונה אז אי אפשר לבצע.

הרבה פעמים ניתן לסדר את המשימות ביותר מאופן תקף אחד. אם נחזור לדוגמה של שגרת הבוקר אז אפשר לעשות מתיחות אחרי שיוצאים מהמיטה ורק אז לצחצח שיניים או קודם לצחצח שיניים ורק אז מתיחות מבחינת המיון הטופולוגי זה לא משנה כי עדיין ניתן לבצע את כל המשימות.

מיון טופולוגי משמש במגוון תרחישים מציאותיים בהם צריך לסדר משימות שתלויות אחת בשנייה באופן בר ביצוע כך שטרם ביצוע משימה מסוימת מבצעים את כל המשימות בהם היא תלויה.

כמה שימושים מעשיים במיון טופולוגי כוללים:

• תלויות בתוכנה: בפיתוח תוכנה, ניהול תלות בין מודולים או ספריות הוא קריטי. מיון טופולוגי יכול לעזור לקבוע את הסדר הנכון בו צריך להעלות את המודולים כדי להבטיח את פעולתה התקינה של התוכנה.
• תזמון משימות: בעת ניהול פרויקט עם מספר משימות שיש להן תלות אחת בשנייה, מיון טופולוגי יכול לשמש לתזמן את המשימות באופן שמבטיח שכל התנאים המוקדמים מתקיימים לפני שממשיכים עם המשימות הבאות.
• קביעת סדר למידה של קורסים: בהקשר אקדמי, מיון טופולוגי יכול להיות מיושם לתכנון תוכניות לימודים לסטודנטים. על ידי ייצוג קורסים כצמתים ותנאים מוקדמים של קורסים כקשתות מכוונות, שימוש במיון טופולוגי יבטיח שסטודנטים יקחו את הקורסים המקדימים הדרושים לפני שהם מתקדמים לקורסים מתקדמים התלויים בהם.
• ניהול פרויקטים: מיון טופולוגי מועיל למנהלי פרויקטים לתכנן ולארגן משימות בפרויקט. זה עוזר להם להבין את הנתיב הקריטי של יישום הפרויקט תוך וידוא שמשימות יתבצעו בסדר הנכון כדי לעמוד בתאריכי היעד.
• ייצור בקו הרכבה: בקווי הרכבה תעשייתיים לעיתים קרובות יש משימות התלויות בהשלמת משימות קודמות. מיון טופולוגי יכול לשמש לאופטימיזציה של התהליך ולוודא זרימה חלקה של הייצור.
• ועוד…

האלגוריתם ע"ש קאהן למיון טופולוגי

הרעיון של האלגוריתם ע"ש קאהן Kahn's algorithm הוא לחזור ולהסיר צמתים שאין להם תלויות מהגרף ולהוסיף אותם לתוצאה שהיא הצמתים הממוינים באופן טופולוגי. בעוד האלגוריתם מתקדם, מוסרים צמתים ללא תלויות מהגרף כולל הקשתות היוצאות מהם מה שיוצר צמתים חדשים ללא תלויות in-degree = 0. חוזרים על הסרת הצמתים ללא קשתות הנכנסות אליהם עד שעוברים על כל הצמתים או עד שנתקלים בהפניות מעגליות. אם נתקלים בהפניות מעגליות אז אי אפשר למיין באופן טופולוגי.

בוא נראה דוגמה למיון טופולוגי של גרף ללא הפניות מעגליות:

נתחיל מבחירה של 1 כיוון שאין לו תלויות (אפשר גם 2), נוסיף אותו לסדר הטופולוגי ונסיר מהגרף:

• הסרה של 1 כוללת את הסרת התלות של 3 בו.

עכשיו יש לנו אפשרות לבחור רק ב-2 כיוון שהוא היחיד שאין לו תלויות (in-bound = 0). נוסיף אותו לסדר הטופולוגי ונסיר מהגרף:

עכשיו נבחר ב-3 כיוון שאין לו תלויות (מאחר והסרנו את 1 ו-2). נוסיף לסדר הטופולוגי ונסיר מהגרף:

בשלב זה אנחנו יכולים לבחור בין שני צמתים ללא תלויות: 4 או 5. נבחר ב-4. נוסיף לסדר הטופולוגי, ונסיר מהגרף:

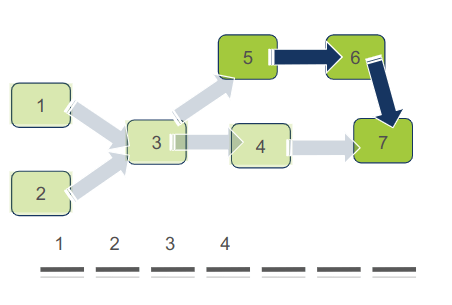
עכשיו אין לנו ברירה אלא להסיר את הצומת היחיד ללא תלויות שהוא 5:

נסיר את 6 שאין לו תלויות בשלב זה:

אחרון חביב. נשארנו עם צומת 7 נטול התלויות. נסיר גם אותו:

קוד פייתון ליישום אלגוריתם קאהן למיון טופולוגי

Kahn הוא שיטה פופולרית למיון טופולוגי של צמתים בגרף מכוון א-מעגלי (DAG). האלגוריתם הוצע על ידי ארתור ב. קאהן בשנת 1962.

האינטואיציה על בסיסה עובד אלגוריתם קאהן הוא שאם למשימה אין תלויות אז אפשר לבצע אותה. לאחר שביצענו את כל המשימות שאין להם תלויות אנחנו יכולים להסיר אותם מהרשימה ולבצע את המשימות שהיו תלויות במשימות שבוצעו, וחוזר חלילה עד שמבצעים את כל המשימות.

שלבי אלגוריתם Kahn הם:

ראשית, מאתחלים רשימה ריקה "רשימת הסדר הטופולוגי" לאחסון הצמתים בסדר טופולוגי.

1. מציאת כל הצמתים בגרף שאין קשתות הנכנסות אליהם (in-degree = 0).

2. הוספת כל הצמתים בגרף שאין קשתות הנכנסות אליהם למבנה נתונים Queue (תור).

3. כל עוד התור אינו ריק, יש לבצע את הפעולות הבאות:

   • הסרת צומת מן התור בתנאי של in-degree = 0.

   • הוספת הצומת לרשימת הסדר הטופולוגי.

   • עבור כל אחד מהצמתים השכנים של הצומת הנוכחי, יש להסיר את הקשת בין הצומת לשכנו מה שיגרום להפחתת in-degree של השכן.

   • במידה וה-in-degree של השכן הופך לאפס לאחר הסרת הקשת המכוונת אליו, יש להכניס גם את השכן לתור.

   • חוזרים על שלב 3 עד לריקון התור.

4. לבסוף, במידה ומספר הצמתים ב-"רשימת הסדר הטופולוגי" שונה ממספר המשימות אז המיון הטופולוגי אינו אפשרי.

להלן הקוד לביצוע אלגוריתם Kahn למיון טופולוגי:

def topological_sort(tasks, prerequisites):
    # Store the neighbors of each task in an adjacency list.
    adj_list = {task: [] for task in tasks}
    
    # Number of in degrees for each task.
    in_degrees = {task: 0 for task in tasks}

    # Fill the adj_list and in_degress within a loop
    for task, dependency in prerequisites:
        adj_list[dependency].append(task)
        in_degrees[task] += 1

    # Queue to keep in line the set of nodes with no incoming edges.
    queue = []
    for task in tasks:
        # 1. Find all nodes with in degree 0.
        # 2. Add these nodes to queue.
        if in_degrees[task] == 0:
            queue.append(task)
    
    # Empty list that will store the topological ordering of nodes
    sorted_tasks = []
    while queue:
        # 3a. Dequeue a node from the queue.
        independent_task = queue.pop(0)
        # 3b. Add the dequeued node to the topological ordering list.
        sorted_tasks.append(independent_task)
        # 3c. For each of the dequeued node's neighboring nodes, 
        # remove the edge between the dequeued node and the neighbor (i.e., reduce the in-degree of the neighbor).
        for neighbor in adj_list[independent_task]:
            if in_degrees[neighbor] > 0:
                in_degrees[neighbor] -= 1
                # 3d. Find all nodes with in degree 0.
                # Add these nodes to queue.
                if in_degrees[neighbor] == 0:
                    queue.append(neighbor)
                    
    # 4. Check that all tasks are in the sorted_tasks list
    if len(sorted_tasks) != len(tasks):
        raise Exception("Cycle detected; Topological ordering isn't possible")

    return sorted_tasks

הפונקציה topological_sort() מבצעת מיון טופולוגי באמצעות אלגוריתם Kahn. הפונקציה מקבלת רשימת משימות (tasks) ואת התלויות שלהם (prerequisites) ומחזירה את המשימות בסדר טופולוגי, במידת האפשר.

נסביר את הקוד:

1. מאתחלים 2 מבני נתונים:

   • מילון adj_list לאחסון התלויות של משימות.
   • מילון in_degrees לאחסון מספר הקשתות הנכנסות (תלויות) של כל משימה.

2. אכלוס מבני הנתונים adj_list ו-in_degrees:

   • עוברים בתוך לולאה על הרשימה prerequisites המכילה טאפלים המייצגים את התלויות בין המשימות. עבור כל תלות (task, dependency), מעדכנים task שיהיה שכן של dependency, ומוסיפים 1 ל-in_degrees עבור ה-task המסויים.

3. מוצאים צמתים שאין להם תלויות (in-degree = 0), ומאתחלים תור Queue.

4. • הקוד נכנס ללולאת while שממשיכה לרוץ עד לריקון התור queue.
   • בכל פעם שהלולאה רצה, היא מוציאה dequeue משימה מחלקו הקדמי של התור.
   • היא מוסיפה את המשימה שעל הפרק לרשימה sorted_tasks.
   • עבור כל צומת שכן של המשימה ע"פ adj_list, היא מקטינה את הדרגה הנכנסת של השכן in-degree ב-1, עקב הסרת התלות והקשתות שיצאו ממנו.
   • אם ה-in-degree של שכן הופכת לאפס בתהליך, זה אומר שהשכן נותר ללא תנאים מוקדמים ולפיכך מוסיפים אותו לתור לצורך עיבוד בהמשך.

5. לאחר שהלולאה סיימה לרוץ, הפונקציה בודקת אם אורך הרשימה sorted_tasks שווה לסך המשימות tasks. אם לא, זה אומר שמיון טופולוגי של המשימות אינו אפשרי. במקרה זה, הקוד זורק exception.

נבחן את הפונקציה topological_sort() לביצוע מיון טופולוגי:

def run_topological_sort_test(tasks, prerequisites):
    try:
        sorted_tasks = topological_sort(tasks, prerequisites)
        print(f"Sorted tasks: {sorted_tasks}")
    except Exception as e:
        print(f"Error: {e}")


if __name__ == "__main__":
    # Task 0: Basic example
    tasks = [1, 2, 3, 4, 5, 6, 7]
    prerequisites = [(3, 1), (3, 2), (5, 3), (4, 3), (6, 5), (7, 4), (7, 6)]
    run_topological_sort_test(tasks, prerequisites)
    
    # Test 0: Basic example with a valid topological order
    tasks = ["work", "breakfast", "dress", "wakeup", "exercise", "teeth", "comb", "bath", ]
    prerequisites = [("teeth", "comb"),
                     ("comb", "bath"),
                     ("bath", "dress"),
                     ("dress", "wakeup"),
                     ("work", "breakfast"), 
                     ("breakfast", "teeth"),
                     ("exercise","wakeup")]
    run_topological_sort_test(tasks, prerequisites)

    # Test 1: Basic example with a valid topological order
    tasks = [0, 1, 2, 3, 4]
    prerequisites = [(1, 0), (2, 1), (3, 2), (4, 3)]
    run_topological_sort_test(tasks, prerequisites)

    # Test 2: Node 4 is independent
    tasks = [0, 1, 2, 3, 4]
    prerequisites = [(1, 0), (2, 1), (3, 2)]
    run_topological_sort_test(tasks, prerequisites)

    # Test 3: Tasks with multiple prerequisites
    tasks = [0, 1, 2, 3, 4]
    prerequisites = [(1, 0), (2, 1), (3, 2), (4, 0), (4, 2)]
    run_topological_sort_test(tasks, prerequisites)

    # Test 4: Tasks with no prerequisites
    tasks = [0, 1, 2, 3, 4]
    prerequisites = []
    run_topological_sort_test(tasks, prerequisites)

    # Test 5: Cyclic dependency
    tasks = [0]
    prerequisites = [(0, 0)]
    run_topological_sort_test(tasks, prerequisites)
    
    # Task 6: Cyclic dependency
    tasks = [0, 1]
    prerequisites = [(1, 0), (0, 1)]
    run_topological_sort_test(tasks, prerequisites)

הערכת ביצועים

סיבוכיות זמן:

• בניית רשימת הקישוריות (adjacency list) ואחסון (in-degree) אורכים O(V + E), כאשר V הוא מספר הצמתים (משימות) ו-E הוא מספר הקשתות (תלויות) בגרף.
• החלק העיקרי של האלגוריתם כרוך בסריקה של כל צומת פעם אחת ועדכון ערכי in-degree של שכניו, מה שדורש O(V + E).
• הבדיקה האם כל הצמתים כלולים בתוצאה הסופית אורכת זמן קבוע.

לכן, זמן הריצה הכולל של פונקציית topological_sort() הוא O(V + E).

סיבוכיות מקום:

• סיבוכיות המקום נקבעת בעיקר על ידי מבני הנתונים המשמשים לאחסון ייצוג הגרף ומשתנים אחרים.
• רשימת הקישוריות (adjacency list) ואחסון (in-degree) לוקחים כל אחד מקום O(V), כאשר V הוא מספר הצמתים (משימות) בגרף.
• התור המשמש באלגוריתם יכול לאחסן לכל היותר V צמתים, כך שהוא לוקח לכל היותר O(V).
• רשימת sorted_tasks מאחסנת את המשימות הממוינות ע"פ סדר טופולוגי, ודורשת לכל היותר O(V).

לכן, סיבוכיות המקום הכוללת של פונקציית topological_sort() היא O(V), כאשר V הוא מספר הצמתים (משימות) בגרף.

לסיכום, סיבוכיות הזמן של הפונקציה היא O(V + E), וסיבוכיות המקום היא O(V).

סיכום

האלגוריתם ע"ש Kahn הוא שיטה פופולרית ויעילה לביצוע מיון טופולוגי של גרף מכוון א-מעגלי (DAG). האלגוריתם מתחיל בזיהוי צמתים ללא קשתות נכנסות ומסיר אותם בהדרגה מהגרף תוך עדכון in-degree של הצמתים השכנים. תהליך זה מבטיח שכל צומת מתוזמן רק לאחר שכל תלויותיו הושלמו. האלגוריתם מסתיים כאשר כל הצמתים מעובדים ומתקבל סדר טופולוגי תקף, או כאשר מתגלה הפנייה מעגלית, מה שמצביע על כך שאין סדר טופולוגי תקף. האלגוריתם ע"ש Kahn משמש לפתרון של מגוון בעיות, כגון תזמון משימות, או תלויות בתוכנה, כאשר סדר הביצוע קריטי להצלחת המשימה.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

יישום תורת הגרפים בפייתון - חלק א

יישום רשימת סמיכויות adjacency list - חלק ב בסדרה על גרפים

Pyviz - ספרייה להצגת גרפים אינטראקטיביים

General Tree data structure עץ נתונים

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים