יישום תורת הגרפים בפייתון - חלק א

מבנה נתונים גרף graph הוא דרך לייצג קשר בין אובייקטים. גרף מורכב מסט של צמתים (nodes) ביניהם מחברות קשתות (edges). משתמשים בגרפים בשביל רשתות חברתיות, ניווט, למידת מכונה, ועוד.

בגרף כל צומת (node, vertex) מייצג אובייקט, כדוגמת אנשים, מקומות, דפי אינטרנט. הקשתות (edges) מחברות בין צמתים וכך הם מייצגות את היחסים בין האובייקטים. גרפים יכולים להיות מכוונים directed בהם הקשתות מייצגות יחס חד-כיווני או לא מכוונים undirected בהם קשתות המבטאות יחס דו-כיווני. בגרף ממושקל weighted graph לקשתות מוצמד ערך המכונה משקל.

בגרפים מכוונים לקשתות יש כיוון אשר עשוי להיות חד כיווני. אם קשת מכוונת מחברת את הצומת A ל-B, וגם A מצביע על B זה לא אומר בהכרח ש-B מצביע על A. דוגמה לגרפים מכוונים הם קישורים בין דפי אינטרנט. כל דף הוא צומת, ובין הדפים מחברים היפרלינקים שהם קשתות בעלות כיוון. אם אני מוציא מדף האינטרנט הזה שאותו אתה קורא קישור לויקיפדיה זה לא מחייב שהם יגמלו לי בקישור.

עבור גרפים בלתי מכוונים היחס בין הצמתים הוא דו כיווני. אם צמתים A ו-B מקושרים אז A מצביע על B וגם B מצביע על A. דוגמה לגרפים בלתי מכוונים היא מערכת החברויות בפייסבוק. אם אנחנו יודעים שאבי הוא חבר של בני אז זה עובד גם הפוך, בני הוא חבר של אבי.

בגרף ממושקל לקשתות יש ערכים, לרוב מספריים המכונים משקלים. לדוגמה, מערכת תעבורה בין עירונית כאשר הערים מיוצגות על ידי צמתים והכבישים הם הקשתות המחברות ביניהם. אפשר להצמיד לכל כביש ערך מספרי המבטא את המרחק בק"מ או את זמן הנסיעה בדקות.

אמרנו שגרפים מורכבים מסט של צמתים (nodes) וקשתות (edges) המחברות ביניהם. אז בוא נהיה יותר פורמליים.

נתון הגרף הבא:

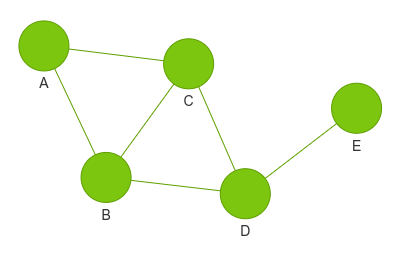
• שהוא גרף בלתי מכוון כיוון שהצמתים הם דו-כיווניים.

סט הצמתים המייצג את הגרף הוא:

V = [A, B, C, D, E]

וסט הקשתות המחברות בין הצמתים הוא:

E = [(A, B), (A, C),  (B, C), (B, D), (C, D), (D, E)]

סה"כ מספר הצמתים:

|V| = 5

סה"כ מספר הקשתות:

|E| = 6

ניתן לייצג כל גרף באמצעות 2 הסטים, סט הקשתות וסט הצמתים:

G = <V, E>

ייצוגים של גרפים

מייצגים גרפים בשני אופנים עיקריים: רשימת סמיכויות Adjacency list ומטריצת סמיכויות Adjacency matrix.

רשימת סמיכויות Adjacency list

נחזור לגרף:

אנחנו רואים שלגרף יש 5 צמתים. נציג אותם:

A
B
C
D
E

לכל צומת יש רשימה של צמתים נוספים הסמוכים אליו. את רשימת הצמתים הסמוכים יתחמו סוגריים מרובעים כי כך מסמלים רשימות של פייתון:

A : []
B : []
C : []
D : []
E : []

הצמתים הסמוכים ל-A הם B ו- C. נוסיף אותם לסכמה:

A : [B, C]
B : []
C : []
D : []
E : []

הצמתים הסמוכים ל-B הם A, C, D אז נוסיף גם אותם:

A : [B, C]
B : [A, C, D]
C : []
D : []
E : []

באופן דומה, נשייך לכל יתר הצמתים את השכנים שלהם:

A : [B, C]
B : [A, C, D]
C : [A, B, D]
D : [B, C, E]
E : [D]

סה"כ המקום הנדרש בזכרון כדי להכיל רשימת סמיכויות adjacency list המייצגת גרף בלתי מכוון הוא מספר הצמתים |V| פלוס פעמיים מספר הקשתות |E| כי הקשתות קשורות בקשר דו כיווני (A מצביע על B וכמו כן B מצביע על A) אבל מכיוון שכאשר משתמשים בשיטת רישום big O נוטים להזניח את הקבועים אז המקום בזיכרון יהיה:

O(|V| + |E|)

מטריצת סמיכויות Adjacency matrix

ניתן לייצג גרף באמצעות מטריצה שאורכה וגובהה כמספר הצמתים:

|V| X |V|

כאשר כל תא במטריצה מייצג קשת פוטנציאלית בין שני צמתים. אם הקשת קיימת ערך התא יהיה 1, אחרת הערך יהיה 0.

נייצג את הגרף הבא המונה 5 צמתים:

באמצעות מטריצה של 5 X 5 תאים:

   | A | B | C | D | E
------------------------
 A |   |   |   |   |
------------------------
 B |   |   |   |   |
------------------------
 C |   |   |   |   |
------------------------
 D |   |   |   |   |
------------------------
 E |   |   |   |   |

• בין צומת A לצומת B יש קשת מחברת ולכן נכתוב 1 בתא.
• בין הצומת A לעצמו אין קשת מחברת ולכן נכתוב בתא 0.

   | A | B | C | D | E
------------------------
 A | 0 | 1 |   |   |
------------------------
 B |   |   |   |   |
------------------------
 C |   |   |   |   |
------------------------
 D |   |   |   |   |
------------------------
 E |   |   |   |   |

A מקושר באמצעות קשת ל-B ול-C. נסמן שני תאים אילו ב-1:

   | A | B | C | D | E
------------------------
 A | 0 | 1 | 1 |   |
------------------------
 B |   |   |   |   |
------------------------
 C |   |   |   |   |
------------------------
 D |   |   |   |   |
------------------------
 E |   |   |   |   |

A אינו מקושר לכל יתר הצמתים. על כן נסמן את כל יתר התאים בשורה של A ב-0:

   | A | B | C | D | E
------------------------
 A | 0 | 1 | 1 | 0 | 0
------------------------
 B |   |   |   |   |
------------------------
 C |   |   |   |   |
------------------------
 D |   |   |   |   |
------------------------
 E |   |   |   |   |

צומת B מקושר עם A, C, D. נציין תאים אילה ב-1 ואת כל היתר בשורה של B נציין ב-0:

   | A | B | C | D | E
------------------------
 A | 0 | 1 | 1 | 0 | 0
------------------------
 B | 1 | 0 | 1 | 1 | 0
------------------------
 C |   |   |   |   |
------------------------
 D |   |   |   |   |
------------------------
 E |   |   |   |   |

• הדרך הפשוטה היא למלא את המטריצה שורה אחר שורה מלמעלה למטה. בכל שורה, קודם כל נכתוב 1 בכל התאים המייצגים קישורים קיימים. אחרי שנסיים למלא את האחדות, נמלא את התאים הנותרים בשורה באפסים.

נמלא את יתר השורות במטריצה:

   | A | B | C | D | E
------------------------
 A | 0 | 1 | 1 | 0 | 0
------------------------
 B | 1 | 0 | 1 | 1 | 0
------------------------
 C | 1 | 1 | 0 | 1 | 0
------------------------
 D | 0 | 1 | 1 | 0 | 1
------------------------
 E | 0 | 0 | 0 | 1 | 0

עבור גרף בלתי מכוון, כמו זה שאנחנו עובדים איתו, גם אם נסובב את המטריצה ב-90 מעלות עדיין נקבל את אותה המטריצה בגלל הקשרים הדו כיווניים. כך שזה לא משנה אם אנחנו הופכים בין הצירים עדיין נקבל את אותו הייצוג.

כמות הזיכרון הדרושה לאחסון גרף באמצעות מטריצה היא ריבוע מספר הצמתים בגרף:

O(|V| X |V|) = O(|V| ^ 2)

הזמן הנדרש לענות על השאלה האם A הוא שכן של B הוא קבוע כשמשתמשים במטריצת סמיכויות כי אורך השורות הוא תמיד V. היתרון של מטריצת סמיכויות הוא עבור גרף המכיל קשתות רבות אבל אם הגרף הוא דליל העדיפות היא לרשימת סמיכויות adjacency list כדי לחסוך בנפח אחסון.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

יישום תורת הגרפים בפייתון - חלק א

יישום רשימת סמיכויות adjacency list - חלק ב בסדרה על גרפים

חלק ג בסדרה על גרפים - Pyviz - ספרייה להצגת גרפים אינטראקטיביים

הבנת אלגוריתם חיפוש לרוחב - BFS - סריקה של גרפים ומציאת הנתיב הקצר ביותר

אלגוריתם חיפוש לעומק DFS - מהבנה ליישום

אלגוריתם דייקסטרה Dijkstra למציאת הנתיב הקצר ביותר בגרף ממושקל

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים