General Tree data structure עץ נתונים
עץ נתונים Tree data structure הוא מבנה נתונים המשמש בתכנות לייצוג מבנים היררכיים. בניגוד לעצים בינאריים, שיש להם לכל היותר שני צמתים ילדים לכל הורה, עץ נתונים כללי מאפשר מספר צמתים ילדים לכל צומת הורה. גמישות זו הופכת אותו למבנה נתונים רב-תכליתי המשמש בין השאר לצורך היררכיות ארגוניות, מערכות קבצים, מבני XML/HTML ועוד.
בעץ כללי, לכל צומת יכולים להיות אפס או יותר צמתים צאצאים. הצומת בראש העץ נקרא השורש, וכל שאר הצמתים מחוברים אליו באמצעות יחסי הורה-ילד. הצמתים שאין להם ילדים ידועים כצמתים עלים. כל צומת בעץ מכיל מידע היכול להיות כל אובייקט או ערך.
אחד היתרונות המרכזיים של עץ כללי הוא יכולתו לייצג מערכות יחסים והיררכיות מורכבות בצורה טבעית ואינטואיטיבית. הוא מאפשר ארגון ואחזור יעיל של נתונים, כמו גם ביצוע פעולות וסריקות traversal המותאמים למבני עצים. תוכל להשתמש בו לייצוג קשרים בין אובייקטים תכנותיים ולתפעל ביעילות יחסים היררכיים בתחום התוכנה.
דוגמה קונקרטית לעץ נתונים היא עץ פילוגנטי. כשרוצים לתאר קשרים בין מינים ביולוגיים משתמשים בעץ פילוגנטי שמקבץ ביחד מינים דומים ומשייך את המינים למשפחות בסדר היררכי הולך ועולה.

- בתרשים העץ לעיל אפשר לראות כיצד כלב בית, כמו השועל וכמו זאב הערבות שייך למשפחת הכלבים, השייכים למשפחת הטורפים, ולסוג יונקים (ההיררכיה הפילוגנטית אינה מדויקת ומובאת לצרכים לימודיים).
הרעיון של עץ היררכי מסתעף מופיעה בעולם המחשבים כמבנה נתונים מסוג "עץ נתונים" Tree data structure. במדריך זה נסביר על מבנה הנתונים, וכיצד ליישם אותו בשפת פייתון.
נחזור לתרשים:

- מה שאפשר לראות בתרשים הוא עץ הפוך על ראשו. הכי למעלה השורש וממנו מתפצלים כלפי מטה ענפי העץ.
במילים יותר מדויקות, אנחנו יכולים לדבר על "עץ נתונים" כעל מבנה היררכי הכולל צמתים nodes וקשתות המקשרות בין צמתים, edges.
במדריך קודם למדנו על רשימה מקושרת linked listשגם בה יש צמתים וקשתות אבל רשימה היא מבנה ליניארי ולא היררכי כי כל החברים ברשימה נמצאים ברמה שווה. בעץ, לעומת זאת, הצמתים מדורגים לפי רמות של מרחק משורש העץ.
אנחנו רואים את השורש המשותף ממנו מתחיל העץ זה ה-root. לשורש יש צאצאים אילו הם ה-node, והכי למטה נמצאים צמתים ללא צאצאים המכונים leaf.
בעולם המחשבים נמצא את מבנה הנתונים עץ Tree data structure כדרך לארגן תיקיות במחשב. כל תיקייה עשויה להתפצל לתיקיות משנה, וכל תיקיית משנה יכולה להתפצל גם היא. התוצאה היא מבנה תיקיות היררכי.
דוגמאות נוספות למבנה נתונים עץ במחשבים הם מסמכי HTML או XML, עצי החלטה בלמידת מכונה (דוגמת מודל XGBOOST), או מודלים לרשתות מחשבים. ואילו רק דוגמאות אחדות. יש רבות נוספות.
כמה מושגים שצריך להכיר הם:
-
צומת, node - עץ הוא אוסף של צמתים nodes. הצמתים מחוברים בקשתות edges.
-
שורש, root node - צומת "שורש" מהווה את נקודת ההתחלה של העץ ממנו מתפצלים כל יתר חלקי העץ. לשורש אין הורה.

-
עלה leaf node - צומת שאין לו צאצאים.
-
צומת (פנימי) inner node - צומת שאינו עלה.
-
ancestors - נמצאים ברמות שמעל לצומת מסוים.
-
descendant צאצאים - נמצאים ברמות אשר מתחת לצומת מסוים.
-
הורים parents - לצומת הורה יש ילד אחד או יותר. הוא נמצא רמה אחת מעל הילדים שלו.

בהגדרות השתמשנו במונח "רמה" level לצורך ביטוי המרחק בין צומת מסוים לבין שורש העץ. השורש נמצא ברמה 0, ולכל רמה מתחתיו מתווסף 1. נחזור לדוגמת עץ המינים שלנו:
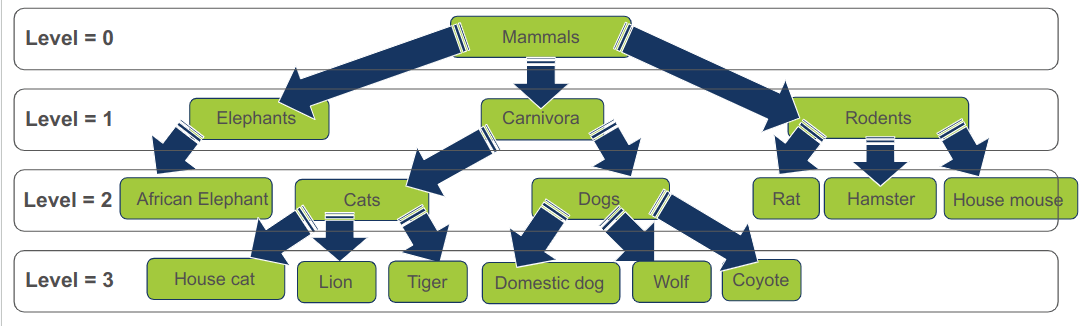
- נעקוב אחר אחד הנתיבים בתרשים כדי להבין את נושא הרמות. ברמה 0 ישנם יונקים, רמה אחת מתחת ישנם טורפים (רמה 1), מתחתם כלבים וחתולים (רמה 2), והכי למטה "חתול בית" ו-"אריה" הנמצאים ברמה 3.
עץ נתונים כמבנה נתונים רקורסיבי
אחת הדרכים המועילות ביותר להבין עץ נתונים היא לחשוב עליו כעל מבנה רקורסיבי שחוזר על עצמו כאשר העץ בנוי מתתי עצים. כל תת עץ הוא עץ בפני עצמו עם שורש והתפצלויות משל עצמו, כמו העץ הראשי.

- כל צומת של עץ נתונים מכיל את המידע מי הילדים שלו. הילדים מכילים מידע על הילדים שלהם, וכך תתי עצים subtrees הם עצים בפני עצמם.
העובדה שעץ נתונים בנוי מתתי עצים מאפשר לפתור בעיה של עץ גדול על ידי פירוק לתתי עצים קטנים מה שמאפשר לטפל בכל אחד מהם כעץ נפרד ואז להתקדם מהעצים הקטנים במעלה ההיררכיה עד שפותרים את העץ המלא. מסיבה זו נראה רקורסיה כפתרון לפונקציות רבות הנדרשות לעבודה עם עצי נתונים כדוגמת: סריקה traversal, איתור, הוספה, מחיקה, וכיו"ב.
יישום עץ נתונים בשפת פייתון
כשאנחנו מדברים על "עץ נתונים" במדריך הנוכחי אנחנו מתייחסים לעץ כללי שבו להורה יכול להיות כל מספר של ילדים. הוא יכול להיות ללא ילדים, יכול להיות לו ילד 1, 2, 3, 10, וכיו"ב. אין הגבלה. ישנו מקרה פרטי של עץ נתונים המכונה "עץ בינארי" שבו לכל צומת יכולים להיות לכל היותר 2 ילדים.
עץ נתונים מורכב מצמתים nodes. כל node צומת הוא עץ בפני עצמו. נקרא לקלאס פייתון המייצג צומת אחד בשם Tree:
class Tree:
def __init__(self, data):
self.data = data
self.parent = None
self.children = []Tree שהוא צומת וגם עץ (מבנה רקורסיבי אמרנו. צריך להתרגל 😄) מכיל 3 שדות:
- data - המידע המוכל בצומת. זה יכול להיות מחרוזת, מספר, אובייקט או מה שנבחר.
- parent - מצביע על ההורה של הצומת הנוכחי. אם ההורה הוא None אז הצומת הוא שורש העץ. לא בכל יישומי העץ תמצאו את השדה הזה.
- children - מחזיק רשימה של צמתים ילדים של הצומת הנוכחי.
נוסיף לקלאס Tree מתודה add_child() להוספת צמתים ילדים לעץ:
class Tree:
def __init__(self, data):
self.data = data
self.parent = None
self.children = []
def add_child(self, child):
child.parent = self
self.children.append(child)נסביר את המתודה add_child() להוספת צומת כילד של הצומת הנוכחי:
-
המתודה מקבלת פרמטר child המייצג את הצומת החדש אותו יש להוסיף כילד של הצומת הנוכחי.
-
שורת הקוד:
child.parent = selfמשמשת להגדרת ההורה של הילד על הצומת הנוכחי self.
-
שורת הקוד הבאה:
self.children.append(child)משמשת לצורך הוספת ה-node החדש child לרשימת הילדים של הצומת הנוכחי self.children
ננסה את המתודה add_child():
ניצור את העץ הראשי על ידי הגדרת השורש שלו אותו נאחסן במשתנה root:
# Create the tree
root = Tree("Mammals")נוסיף ילד לצומת root בשני שלבים:
car = Tree("Carnivora")
root.add_child(car)- נגדיר צומת חדש באמצעות אתחול הקלאס Tree (תזכורת כל צומת בעץ נתונים הוא עץ נתונים בפני עצמו).
- באמצעות המתודה add_child() של ה-root נוסיף את הצומת החדש בתור ילד של ה-root.
נוסיף עוד שני ילדים גם כן באמצעות המתודה add_child(). גם אותם נגדיר כילדים של הצומת root:
ele = Tree("Elephants")
root.add_child(ele)rod = Tree("Rodents")
root.add_child(rod)גם הילדים הם עץ עם תכונות ומתודות של עץ. אם כך, אנחנו יכולים להשתמש גם עליהם במתודה add_child() כדי להגדיר להם ילדים. לדוגמה, להגדיר ילד "dogs" של הצומת "carnivora" (=טורף):
dogs = Tree("Dogs")
car.add_child(dogs)אותו פטנט יעבוד גם על הצומת "cats" שגם הוא ילד של "carnivora". נוסיף את הצומת:
cats = Tree("Cats")
car.add_child(cats)אחרי שהסברנו נוסיף את כל הצמתים לעץ הנתונים תוך הקפדה על שמירת המבנה ההיררכי הודות לשיוך הצמתים להורים הישירים שלהם:
# Create the tree
root = Tree("Mammals")
ele = Tree("Elephants")
root.add_child(ele)
afe = Tree("African elephant")
ele.add_child(afe)
car = Tree("Carnivora")
root.add_child(car)
dogs = Tree("Dogs")
car.add_child(dogs)
dog = Tree("Domestic_dog")
dogs.add_child(dog)
wolf = Tree("Wolf")
dogs.add_child(wolf)
coy = Tree("Coyote")
dogs.add_child(coy)
fox = Tree("Fox")
dogs.add_child(fox)
cats = Tree("Cats")
car.add_child(cats)
cat = Tree("Domestic_cat")
cats.add_child(cat)
lion = Tree("Lion")
cats.add_child(lion)
tiger = Tree("Tiger")
cats.add_child(tiger)
rod = Tree("Rodents")
root.add_child(rod)
hm = Tree("House_mouse")
rod.add_child(hm)
rat = Tree("Rat")
rod.add_child(rat)
ham = Tree("Hamster")
rod.add_child(ham)
- יש לנו עץ.
נדפיס את העץ בעזרת מתודה print_tree() אותה נוסיף לקלאס Tree:
def print_tree(self):
print(self.data)לכל צומת יכולים להיות ילדים. נוסיף למתודה print_tree() קוד להדפסת הילדים:
def print_tree(self):
# Print current node
print(self.data)
# Print current node children
for child in self.children:
print(child.data)גם לילדים יש ילדים משלהם, שהם נכדים של ה-root וגם לנכדים יכולים להיות ילדים וחוזר חלילה. אז במקום להסתבך ולכתוב פונקציה להדפסה לכל רמה נוספת של צאצאים, כזו שקיימת וכזו שאולי נוסיף בעתיד, אנחנו יכולים להשתמש ברקורסיה לצורך קריאה למתודה המדפיסה עבור הילדים:
def print_tree(self):
# Print current node
print(self.data)
# Print current node children
for child in self.children:
# Call the method recursively from within the method
child.print_tree()נקרא לפונקציה כדי שתדפיס את העץ:
root.print_tree()התוצאה:
Mammals Elephants African elephant Carnivora Dogs Domestic_dog Wolf Coyote Fox Cats Domestic_cat Lion Tiger Rodents House_mouse Rat Hamster
- התוצאה כוללת את המידע מכל הצמתים כך שאנחנו יכולים לסמוך על הרקורסיה שעושה את העבודה. אבל מה שקיבלנו זו רשימה. ההיררכיה הלכה לאיבוד בצורת ההצגה הזו.
כדי לפתור את הבעיה מקובלת צורת הצגה שבה צמתים המרוחקים מהשורש מוזחים ימינה. כאשר מידת ההזחה הולכת וגדלה ככל שהצומת רחוק יותר מהשורש. בשביל לדעת את המרחק של צומת מהשורש אנחנו צריכים מתודה שתדע באיזו רמה של העץ נמצא כל צומת. לשם כך, נוסיף את המתודה get_level() למציאת הרמה של צמתים לקלאס Tree:
def get_level(self):
# Start with the current node's level as 0
current_level = 0- הפונקציה מתחילה לספור את הרמות מהצומת הנוכחי המוגדר self שה-level שלו הוא 0.
כדי להסיק באיזו רמה של העץ נמצא הצומת אנחנו צריכים ללכת אחורה - להתחיל מההורה של הצומת הנוכחי ומשם להורה של הצומת ההורה וחוזר חלילה. אפשר לעשות את זה עם רקורסיה. אבל אנחנו נעשה את זה באמצעות איטרציה (עם לולאה) כי באופן כללי איטרציה צורכת פחות משאבים מרקורסיה:
def get_level(self):
# Start with the current node's level as 0
current_level = 0
# Traverse upwards until reaching the root node (where current_parent is None)
current_parent = self.parent
while current_parent:
# Increment the level for each parent node
current_level += 1
current_parent = current_parent.parent
# Return the calculated level of the current node
return current_level- המתודה עוברת על ההורים בתוך לולאה לפי סדר ההיררכיה - מההורה הישיר, להורה שמעליו, וכיו"ב עד שמגיעים להורה שהוא root שאין לו הורה משל עצמו. ב-root הלולאה תפסיק לרוץ כי בהגדרה ההורה של root הוא None.
נוודא שהמתודה get_level() עובדת:
print(root.get_level())
print(car.get_level())
print(dogs.get_level())
print(coy.get_level())התוצאה:
0 1 2 3
- "root" הוא ברמה 0, וזאב הערבות "coyote" הוא ברמה 3. גם שני האחרים נכונים. המתודה עובדת כמצופה.
נשתמש במתודה get_level() כדי לקבל את רמת הצאצא ואז להוסיף מספר רווחים גדול יותר לצאצאים רחוקים יותר מהשורש:
def print_tree(self):
# Determine the appropriate prefix for the node based on its level
# If the node has a parent, set the prefix as 'level * space |__'
# Otherwise, set an empty string as the prefix
prefix = f"{self.get_level() * ' '}|__" if self.parent else ""
# Print the node with the appropriate prefix
print(f"{prefix}{self.data}")
for child in self.children:
# Iterate over each child node
# Recursively print the subtree of each child
child.print_tree()ננסה את המתודה על root של עץ מקוצר:
# Create the tree
root = Tree("Mammals")
ele = Tree("Elephants")
root.add_child(ele)
afe = Tree("African elephant")
ele.add_child(afe)
# Print the tree with the revised method
root.print_tree()התוצאה:
Mammals |__Elephants |__African elephant
- אפשר לראות שהמבנה ההיררכי נשמר.
הרצתי את המתודה על העץ כולו, וקיבלתי את התוצאה הבאה:
Mammals |__Elephants |__African elephant |__Carnivora |__Dogs |__Domestic_dog |__Wolf |__Coyote |__Fox |__Cats |__Domestic_cat |__Lion |__Tiger |__Rodents |__House_mouse |__Rat |__Hamster
- בוא נראה. לדוגמה, מתחת ליונקים ישנם טורפים carnivora תחתם חתולים וכלבים, ומתחת לכלבים: כלבי בית, סוגי זאב, שועלים. אפשר לעבור כך על כל אחד מהמקרים…
- יופי 😄
הזכרנו כבר את העובדה שפתרון תכנותי המשתמש בשיטה איטרטיבית יציג לרוב ביצועים טובים יותר מפתרון מקביל המשתמש בשיטה רקורסיבית. אמנם רקורסיה עשויה להיות אינטואיטיבית ליישום מבנים רקורסיביים דוגמת עץ וכך להקל על המתכנת, אבל היא צורכת יותר משאבי מחשוב בגלל העלות המצטברת של ריבוי קריאות לפונקציה מה שעלול להידרדר לכדי הצפת הזיכרון, stack overflow.
בשביל לייעל את המתודה print_tree() נשכתב אותה שתהיה איטרטיבית במקום רקורסיבית. לצורך יישום השיטה האיטרטיבית נשתמש במבנה נתונים "ערימה" stack כי אנחנו רוצים שהאחרון שנכנס יהיה הראשון לצאת כדי לשמור על הסדר:
from collections import deque
def print_tree(self):
# Create a stack with the root node as the starting point
stack = deque([self])
while stack:
# Pop the top node from the stack
node = stack.pop()
prefix = f"{node.get_level() * ' '}|__" if node.parent else ""
# Print the node with the appropriate prefix
print(f"{prefix}{node.data}")
# Push the children of the current node to the stack
stack.extend(reversed(node.children))-
ראשית, ניצור stack "ערימה" שיש בו בתור התחלה רק צומת אחד, self:
stack = [self] -
לולאת while תמשיך לרוץ עד לריקון הערימה, משמע הקוד הדפיס את כל הצמתים.
-
בתוך הלולאה, ישנו קוד המסיר את הצומת אשר בראש הערימה ומציב אותו בתור ערכו של המשתנה node שהוא הצומת הנוכחי:
node = stack.pop() -
הצומת הנוכחי מודפס כפי שראינו ביישום הקודם של המתודה המדפיסה:
prefix = f"{node.get_level() * ' '}|__" if node.parent else "" print(f"{prefix}{node.data}") -
הקוד מוסיף את הילדים של הצומת הנוכחי לתוך הערימה:
stack.extend(node.children)קוד זה שקול להוספת הילדים בתוך לולאה:
# Push the children of the current node to the stack for child in node.children: stack.append(child) -
שימוש במתודה של פייתון reversed() הופכת את סדר ההכנסה של הילדים ל-stack מה שאומר סדר הוצאה נכון אח"כ מה-stack:
stack.extend(reversed(node.children))
על ידי שימוש בשיטה איטרטיבית מבוססת ערימה stack, הצלחנו למנוע שימוש ברקורסיה, ועל ידי כך הפחתנו את צריכת משאבי הזכרון המוגברת, תוצאה של קריאות חוזרות ונשנות לפונקציה בשיטה הרקורסיבית. הגישה האיטרטיבית עדיפה במקרים של עצים גדולים בהם זכרון ה-stack של המחשב עלול להוות גורם מגביל. הגישה הרקורסיבית, לעומת זאת, היא נוחה יותר לתכנות ולהבנה כיוון שמבנה נתונים עץ הוא בעל טבע רקורסיבי.
סריקת עץ Tree traversal
עד עכשיו עשינו את זה אבל לא טרחנו להסביר אז הגיע הזמן. סריקת עץ tree traversal (=מעבר) היא תהליך שבו מבקרים בצמתים של העץ באופן שיטתי, פעם אחת לכל צומת. השתמשנו בתהליך סריקת עץ לצורך הדפסה ועוד נמשיך להשתמש בו כדי לנתח ולעשות מניפולציות של עצים.
במדריך זה נסביר וניישם שתי אסטרטגיות לסריקת עצים: BFS ו-DFS.
-
Depth-First Search (DFS) - הוא אלגוריתם לסריקת גרפים (בהם גם עצים) שסורק הכי רחוק שהוא יכול לאורך כל ענף של עץ לפני שהוא פונה לאחור להשלים את מלאכת הסריקה של ענפים שהוא עוד לא ביקר בהם. האלגוריתם כולל שני צעדים:
- ביקור בצומת הנוכחי.
- סריקה של כל ילד של הצומת הנוכחי.
ניתן ליישם את אלגוריתם DFS בשיטה רקורסיבית או איטרטיבית. יישום איטרטיבי של DFS משתמש במבנה נתונים "ערימה" stack.
נשתמש באסטרטגיה DFS לסריקת עצים כשאנחנו מעוניינים לחפש צומת או נתיב מסוימים, לבדוק קישוריות בין צמתים או לצורך חקירת/תיאור מבנה העץ. את המתודה print_tree() ביססנו על אלגוריתם DFS.
-
Breadth-First Search (BFS) - הוא אלגוריתם לסריקת גרפים (בהם גם עצים) הסורק את העץ על ידי ביקור שיטתי של כל הצמתים ברמה הנוכחית לפני שהוא עובר לרמה הבאה. האלגוריתם כולל שני צעדים:
- הוספת צומת השורש של העץ למבנה נתונים "תור" queue.
- כל עוד התור אינו ריק יש להסיר את הפריט הראשון ולבקר בו, וחוזר חלילה עד שהתור מתרוקן לחלוטין מצמתים.
BFS משתמש במבנה נתונים queue לקביעת סדר הטיפול בצמתים. הדרך הנפוצה ליישום BFS משתמשת באיטרציה.
נשתמש באסטרטגיה BFS לסריקת עצים כדי למצוא את הנתיב הקצר ביותר ולסריקה של עצים רמה אחר רמה.
מכיוון שאנחנו יודעים איך לכתוב קוד המיישם DFS באופן יעיל בשיטה איטרטיבית נכתוב פונקציה נוספת get_size() המבוססת על DFS שתפקידה למנות את מספר הצמתים בעץ:
from collections import deque
def get_size(self):
# Variable to keep track of the node count
node_count = 0
# Initialize the stack with the root node
stack = deque([self])
while stack:
node = stack.pop()
# Increment the node count for each visited node
node_count += 1
# Add children to the stack for further processing
stack.extend(node.children)
return node_countנבדוק:
print(root.get_size())התוצאה 17.
נסביר את המתודה get_size():
- המתודה מגדירה מונה צמתים node_count שערכו ההתחלתי 0.
- המתודה סורקת את העץ בשיטת DFS לצורך כך היא משתמש ב-stack.
- הלולאה רצה כל עוד ה-stack אינו מרוקן. ה-stack מרוקן רק בתנאי שהאלגוריתם ביקר את כל הצמתים.
- בכל פעם שהלולאה רצה היא מטפלת בצומת אחד; היא מוסיפה 1 למונה הצמתים node_count.
- הפונקציה מחזירה את מונה הצמתים כשהיא מסיימת לרוץ.
אנחנו יכולים ליישם את המתודה get_size() גם על בסיס אלגוריתם BFS. לשם כך נחליף את מבנה הנתונים "ערימה" stack במבנה הנתונים "תור" queue:
from collections import deque
def get_size(self):
node_count = 0
# Initialize the queue with the root node
q = deque([self])
while q:
# Dequeue the first queue element - FIFO
node = q.popleft()
node_count += 1
# Enqueue the children of the current node
q.extend(node.children)
return node_count
את העץ הדפסנו תוך שאנו מתבססים על DFS. היישום השני של get_size() משתמש ב-BFS. מעניין לראות כיצד יושפע סדר סקירת העץ tree traversal. כדי לבדוק את ההשפעה ביישום הבא של get_size() הוספתי קוד להדפסת צמתים:
def get_size(self):
node_count = 0
# Queue based BFS
q = deque([self])
while q:
node = q.popleft()
node_count += 1
prefix = f"{node.get_level() * ' '}|__" if node.parent else ""
# Print the node with the appropriate prefix
print(f"{prefix}{node.data}")
q.extend(node.children)
return node_countנריץ את הפונקציה:
root.get_size()התוצאה:
Mammals |__Elephants |__Carnivora |__Rodents |__African elephant |__Dogs |__Cats |__House_mouse |__Rat |__Hamster |__Domestic_dog |__Wolf |__Coyote |__Fox |__Domestic_cat |__Lion |__Tiger
- תוצאת הרצת הפונקציה get_size() המשתמשת באלגוריתם BFS ומדפיסה את הצמתים על פי סדר מעבר FIFO היא הדפסה של העץ רמה אחר רמה. קודם כל שורש (mammals), אח"כ רמה ראשונה (Elephants, Carnivora, Rodents) , אח"כ רמה שנייה, וכיו"ב עד שמדפיסים את כל הצמתים. השוואה של תוצאה זו למתודה print_tree() מבוססת אלגוריתם DFS מלמדת אותנו על סדר הסקירה השונה בין DFS ל-BFS.
חיפוש של צומת
אפשר למצוא צמתים מסוימים של העץ תוך שמתבססים על אלגוריתמים BFS או DFS. אם רוצים לחפש כמה שיותר קרוב לשורש העץ אז עדיף BFS כי הוא מחפש רמה אחר רמה החל מרמת השורש. DFS, לעומתו, עדיף אם הצומת המבוקש נמצא עמוק בתוך העץ או שמחפשים נתיב path (גם לזה נגיע). הסיבה להעדיף את DFS היא שהוא סוקר כמה שיותר עמוק לפני שהוא חוזר על עקבותיו, ולכן הוא מתחיל מהקצוות של העץ מה-leaves הנמצאים הכי רחוק מהשורש.
ניישם את המתודה find_node() לחיפוש של צומת תוך התבססות על אלגוריתם DFS :
def find_node(self, node):
# Stack to be filled with the iterations (DFS)
stack = deque([self])
while stack:
# Remove the top-most element from the stack
current = stack.pop()
if current == node:
# If the current node's data matches the target value, return the current node
return node
# Add the children of the current node to the stack
stack.extend(reversed(current.children))
# If no match is found, return an empty node instance
return Tree(None)ננסה את הפונקציה:
res = root.find_node(ham)
print(res.data)התוצאה:
Hamster
ניסיתי גם לחפש מידע שלא קיים בעץ, וקיבלתי את התוצאה None כמצופה:
zeb = Tree("Zebra")
res = root.find_node(zeb)
print(res.data)התוצאה:
None
נסביר.
המתודה find_node() מחפשת node בתוך העץ תוך שימוש באלגוריתם DFS שבודק כל צומת וממשיך יותר ויותר פנימה אל תוך העץ לפני שהוא חוזר על עקבותיו. אם נמצאת התאמה לצומת אז הצומת מוחזר. אם לא נמצאת התאמה מוחזר צומת ריק.
נסביר את המתודה find_node() שלב אחר שלב:
- את מבנה הנתונים "ערימה" stack מאתחלים עם צומת השורש self.
- לולאת while ממשיכה לרוץ עד לריקון ה-stack. דבר המעיד על ביקור בכל הצמתים.
- בתוך הלולאה, הצומת בראש הערימה מוסר ומוצב בתור ערכו של המשתנה node.
- אם ה-node הנוכחי הוא מה שמחפשים, מוחזר הצומת הנוכחי.
- אם הצומת הנוכחי הוא לא מה שמחפשים, מוסיפים את הילדים שלו ל-stack.
- הלולאה תמשיך לרוץ עד למציאת התאמה או עד שמסיימים לבקר בכל הצמתים.
- אם הלולאה סיימה לרוץ ולא נמצאה התאמה, המתודה תחזיר אובייקט צומת ריק.
מציאת ההורים ancestors של צומת בעץ
עסקנו רבות בסקירת עצים בשיטת BFS ו-DFS. בגדול, ראינו ש-BFS מיושם באופן איטרטיבי באמצעות queue ו-DFS יכול להיות מיושם באופן רקורסיבי או איטרטיבי. בשביל יישום איטרטיבי של DFS נשתמש ב-stack. אבל אין חובה להשתמש ב-stack באופן מפורש. תלוי ביישום. ניישם מתודה get_ancestors() למציאת כל ההורים של הצומת הנוכחי באמצעות DFS בלי להשתמש ב-stack באופן מפורש:
def get_ancestors(self):
# Initialize an empty list to store the ancestors
ancestors = []
current = self
# Check if the current node has a parent
while current.parent:
# Append the parent of the current node to the ancestors list
ancestors.append(current.parent)
# Update the current node to its parent
current = current.parent
# Return the list of ancestors
return ancestorsנבדוק:
ancestors = root.get_ancestors()
if ancestors:
for ancestor in ancestors:
print(ancestor.data)
else:
print([])התוצאה:
[]
ancestors = cat.get_ancestors()
if ancestors:
for ancestor in ancestors:
print(ancestor.data)
else:
print([])התוצאה:
Cats Carnivora Mammals
נסביר את המתודה get_ancestors() המחזירה את רשימת ההורים של צומת בעץ:
- אומנם אנחנו לא רואים stack ביישום המתודה אבל זה לא אומר שאנחנו לא משתמשים ב-DFS. בפועל, המתודה עוקבת אחר המצביע על ההורה של כל צומת ובכך היא סורקת כל נתיב הכי רחוק שהיא יכולה שזה המהות של DFS.
- מאתחלים את המערך ancestors.
- הלולאה while בודקת האם לצומת הנוכחי קיים הורה. אם יש הורה, המשמעות היא שצריך לעבד הורים נוספים.
- כל פעם שהלולאה רצה, מתווסף הורה למערך ancestors. לאחר מכן, הצומת הנוכחי מתעדכן להורה שלו, מה שגורם ללולאה להמשיך לרוץ.
- כשהלולאה מסיימת לרוץ משמעות הדבר שאין יותר הורים כי הגענו לשורש העץ אז מחזירים את המערך ancestors.
מציאת הגובה height של צומת node
גובה של צומת height of a node מוגדר כמספר המרבי של הצמתים בנתיב הארוך ביותר מצומת לעלה leaf node. נשתמש ב-DFS רקורסיבי כדי להסיק את הגובה של צומת בעץ:
def get_height(self):
# Initialize the maximum height
max_height = -1
# Iterate over each child node
for child in self.children:
# Recursively calculate the height of each child
# and update the maximum height if a taller height is found
max_height = max(max_height, child.get_height())
# Increment the maximum height by 1 to account for the current node
return max_height + 1ננסה את המתודה get_height():
print(root.get_height()) # 3
print(cat.get_height()) # 0נסביר את המתודה get_height():
- המתודה מיישמת DFS באמצעות רקורסיה כיוון שהיא סוקרת את עומק העץ לפני שהיא חוזרת.
- המשתנה max_height משמש למעקב אחר גובה העץ. ערכו ההתחלתי הוא -1 כדי שאם ל-node לא יהיו ילדים השלב הסופי return max_height + 1 יבטיח החזרה של ערך 0.
- המתודה מפעילה לולאת for שמתוכה נעשית קריאה רקורסיבית למתודה get_height() עבור כל צומת ילד.
- אם המתודה מוצאת נתיב ארוך יותר מ- max_height היא מעדכנת את ערכו של max_height.
- לבסוף, לערך של max_height נוסיף 1 כדי להתאים לרמה של הצומת הנוכחי.
מחיקה של צומת מעץ נתונים
המתודה delete() מוחקת צומת מעץ נתונים:
def delete(self):
# 1. Validation
if not self.parent:
raise Exception("Cannot delete the root of a tree or a detached node")
# 2. Attach self.children to self.parent
for child in self.children:
self.parent.children.append(child)
child.parent = self.parent
# 3. Detach node from parent
if self in self.parent.children:
self.parent.children.remove(self)
# 4. Clean from memory
self.data = None
self.parent = None
self.children = []-
המתודה בודקת אם הצומת הוא שורש העץ או צומת יתום (ללא הורה). אם זה המצב, היא זורקת exception:
if self.parent is None: # Edge case when trying to delete the root of a tree or a detached node raise Exception("Cannot delete the root of a tree or a detached node") -
אם לצומת יש ילדים, הקוד עובר עליהם באופן שיטתי ומחבר ישירות להורה של הצומת שיש למחוק. צעד זה נועד לשמור על הילדים בתוך מבנה העץ:
# If node has children, attach children directly to parent for child in self.children: self.parent.children.append(child) child.parent = self.parent -
בהמשך, הצומת מוסר מרשימת הילדים של ההורה:
# Detach node from parent if self in self.parent.children: self.parent.children.remove(self) -
לבסוף, מנקים את הצומת מהזיכרון:
# Clean node from memory self.data = None self.parent = None self.children = []
ננסה את המתודה:
dogs.delete()
rod.delete()
cats.delete()
ele.delete()
car.delete()
rat.delete()
# print after the multiple deletions
root.print_tree()התוצאה:
Mammals |_House_mouse |_Hamster |_African elephant |_Domestic_dog |_Wolf |_Coyote |_Fox |_Domestic_cat |_Lion |_Tiger
ננסה למחוק את ה-root:
root.delete()דבר שיגרום לזריקת Exception
מציאת ההורה המשותף הנמוך ביותר Lowest common ancestor
ההורה המשותף הנמוך ביותר Lowest common ancestor (LCA) מתייחס להורה משותף לשני צמתים שהוא צומת הממוקם הכי רחוק מהשורש. כדי למצוא LCA נסרוק את העץ בעזרת רקורסיה.
נוסיף לקלאס Tree את המתודה למציאת LCA של שני צמתים (node1, node2):
def find_lca(self, node1, node2):
# Check if the current node is None or matches either of the input nodes
if self is None or self is node1 or self is node2:
return self
# List to store potential LCA candidates found in child nodes
lca_candidates = []
# Traverse the children of the current node
for child in self.children:
# Recursively call find_lca on each child
lca = child.find_lca(node1, node2)
# If a potential LCA is found in the child node, add it to the candidates list
if lca is not None:
lca_candidates.append(lca)
# Check the number of LCA candidates found
if len(lca_candidates) == 2:
# If both input nodes are found in different subtrees, return the current node as the LCA
return self
elif len(lca_candidates) == 1:
# If only one input node is found, return the LCA candidate found in the child node
return lca_candidates[0]
# If no LCA candidate is found, return None
return Noneנבדוק מה ההורה המשותף של כלב וחתול:
lca = root.find_lca(cat, dog)
if lca is not None:
print("Lowest Common Ancestor:", lca.data)
else:
print("No Lowest Common Ancestor found.")התוצאה:
Lowest Common Ancestor: Carnivora
מה ההורה המשותף לכלב וזאב ערבות?
lca = root.find_lca(coy, dog)
if lca is not None:
print("Lowest Common Ancestor:", lca.data)
else:
print("No Lowest Common Ancestor found.")התוצאה:
Lowest Common Ancestor: Dogs
מה ההורה המשותף לכלב בית ולמשפחת הכלביים?
lca = root.find_lca(dogs, dog)
if lca is not None:
print("Lowest Common Ancestor:", lca.data)
else:
print("No Lowest Common Ancestor found.")התוצאה:
Lowest Common Ancestor: Dogs
נבדוק עוד מספר מקרי קצה:
lca = root.find_lca(dog, afe)
if lca is not None:
print("Lowest Common Ancestor:", lca.data)
else:
print("No Lowest Common Ancestor found.")
lca = root.find_lca(dogs, dogs)
if lca is not None:
print("Lowest Common Ancestor:", lca.data)
else:
print("No Lowest Common Ancestor found.")
lca = root.find_lca(root, root)
if lca is not None:
print("Lowest Common Ancestor:", lca.data)
else:
print("No Lowest Common Ancestor found.")התוצאה:
Lowest Common Ancestor: Mammals Lowest Common Ancestor: Dogs Lowest Common Ancestor: Mammals
נסביר את המתודה find_lca() המשתמשת ברקורסיה למציאת הורה משותף נמוך ביותר של שני צמתים בעץ נתונים, LCA:
- המתודה מקבלת שני קלטים node1 ו-node2 בתור צמתים של העץ שיש למצוא להם את ההורה המשותף הנמוך ביותר.
- המתודה קודם כל בודקת אם הצומת הנוכחי self הוא None או שווה לאחד הצמתים node1 או node2. אם זה המצב, הצומת הנוכחי מוחזר בתור מועמד להיות LCA.
- בהמשך, המתודה יוצרת רשימה ריקה lca_candidates לאחסון המועמדים העשויים להיות LCA שנמצאים בצמתים הילדים של הצומת הנוכחי.
- המתודה עוברת על כל ילד של הצומת הנוכחי בתוך לולאה. עבור כל ילד, מתבצעת קריאה רקורסיבית למתודה find_lca() הכוללת את הפרמטרים node1 ו-node2. אם המתודה מוצאת LCA פוטנציאלי בצומת ילד (משמע, הערך המוחזר מהקריאה הרקורסיבית אינו None), היא מוסיפה צומת זה לרשימה lca_candidates.
-
אחרי שהיא סורקת את כל הילדים, המתודה בודקת כמה מועמדים להיות LCA היא מצאה:
- אם היא מוצאת 2 מועמדים, משמעות הדבר ששתי המטרות, node1 ו-node2, נמצאות בשני תתי עץ אחרים של הצומת הנוכחי, ולפיכך הצומת הנוכחי הוא LCA, אותו תחזיר המתודה.
- אם היא מוצאת מועמד 1 אז המתודה תחזיר מועמד זה כ-LCA.
- אם המתודה לא מצאה מועמדים היא תחזיר None כי אף אחד משני הקלטים לא נמצא בעץ.
סיכום
במדריך זה, למדנו את המושגים הבסיסיים של עץ כמבנה נתונים. למדנו שמבנה נתונים עץ מאפשר מספר נבחר של צמתים ילדים, מה שהופך אותו לכלי גמיש במיוחד לייצוג יחסים היררכיים. דנו במרכיבי המפתח של עץ, כולל השורש, הצמתים והעלים, והבנו כיצד הם מחוברים זה לזה כדי ליצור מבנה מסועף.
לאורך המדריך, כיסינו פעולות חיוניות ואלגוריתמים הקשורים לעצים כלליים. בחנו טכניקות סריקת עצים כמו חיפוש עומק (DFS) וחיפוש רוחב (BFS), המאפשרות לנו לחקור ולגשת לצמתים בצורה שיטתית. כמו כן, חקרנו שיטות למציאת תכונות עצים נפוצות, כגון גובה העץ והאב הקדמון המשותף הנמוך ביותר (LCA) של שני צמתים.
הבנת המושגים והטכניקות המוצגות במדריך זה, יתנו לך בסיס לעבודה עם מבנה נתונים עץ. אתה יכול למנף את הידע הזה כדי לפתור בעיות שונות הכוללות מבנים היררכיים וליישם אלגוריתמים יעילים למניפולציה וניתוח עצים.
זכור, מבנה הנתונים עץ הוא לא רק מושג תיאורטי אלא גם כלי מעשי בשימוש נרחב בפיתוח תוכנה. שימוש בכלי יאפשר לך לייצג מערכות יחסים מורכבות בצורה ברורה ויעילה. ככל שתעמיק ללמוד על עצים תכיר יישומים נוספים שיאפשרו לך לנצל את מלוא הפוטנציאל של עצים כלליים לצורך פתרון בעיות בעולם האמיתי.
מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך
Linked list - רשימה מקושרת - תיאוריה, קוד ואתגרים תכנותיים
יישום רשימת סמיכויות adjacency list - חלק ב בסדרה על גרפים
Linked list - רשימה מקושרת - תיאוריה, קוד ואתגרים תכנותיים
לכל המדריכים בסדרה ללימוד פייתון
אהבתם? לא אהבתם? דרגו!
0 הצבעות, ממוצע 0 מתוך 5 כוכבים


המדריכים באתר עוסקים בנושאי תכנות ופיתוח אישי. הקוד שמוצג משמש להדגמה ולצרכי לימוד. התוכן והקוד המוצגים באתר נבדקו בקפידה ונמצאו תקינים. אבל ייתכן ששימוש במערכות שונות, דוגמת דפדפן או מערכת הפעלה שונה ולאור השינויים הטכנולוגיים התכופים בעולם שבו אנו חיים יגרום לתוצאות שונות מהמצופה. בכל מקרה, אין בעל האתר נושא באחריות לכל שיבוש או שימוש לא אחראי בתכנים הלימודיים באתר.
למרות האמור לעיל, ומתוך רצון טוב, אם נתקלת בקשיים ביישום הקוד באתר מפאת מה שנראה לך כשגיאה או כחוסר עקביות נא להשאיר תגובה עם פירוט הבעיה באזור התגובות בתחתית המדריכים. זה יכול לעזור למשתמשים אחרים שנתקלו באותה בעיה ואם אני רואה שהבעיה עקרונית אני עשוי לערוך התאמה במדריך או להסיר אותו כדי להימנע מהטעיית הציבור.
שימו לב! הסקריפטים במדריכים מיועדים למטרות לימוד בלבד. כשאתם עובדים על הפרויקטים שלכם אתם צריכים להשתמש בספריות וסביבות פיתוח מוכחות, מהירות ובטוחות.
המשתמש באתר צריך להיות מודע לכך שאם וכאשר הוא מפתח קוד בשביל פרויקט הוא חייב לשים לב ולהשתמש בסביבת הפיתוח המתאימה ביותר, הבטוחה ביותר, היעילה ביותר וכמובן שהוא צריך לבדוק את הקוד בהיבטים של יעילות ואבטחה. מי אמר שלהיות מפתח זו עבודה קלה ?
השימוש שלך באתר מהווה ראייה להסכמתך עם הכללים והתקנות שנוסחו בהסכם תנאי השימוש.