Linked list - רשימה מקושרת - תיאוריה, קוד ואתגרים תכנותיים
Linked list "רשימה מקושרת" היא מבנה נתונים פשוט למדי המורכב מאיברים nodes כשכל איבר מצביע refers על האיבר הבא ברשימה, והאיבר האחרון מצביע על "שום דבר" (Null).
היתרון הגדול של רשימה מקושרת נובע מאופייה הדינמי. בניגוד למערכים, אורכם של רשימות מקושרות יכול להתרחב או להתכווץ בלי לדרוש הקצאת מקום בזיכרון מראש. הגמישות הזו הופכת את הרשימה לפתרון אותו יש לשקול עבור מקרים בהם מספר הנתונים עשוי להשתנות בחדות לאורך זמן.
ניתן להשתמש ברשימות מקושרות Linked lists על מנת ליישם מבני נתונים אחרים דוגמת: stacks ערימות, queues תורים, ומילונים dictionaries.
חסרון משמעותי של רשימה מקושרת היא שכדי לגשת לפריטים שאינם בראש הרשימה צריך לעבור אחד - אחד, באופן סדרתי, על האיברים הקודמים. במערכים, לעומת זאת, אפשר לגשת לכל פריט באופן מיידי אם יודעים את האינדקס שלו. מטעם זה לא ניתן להפעיל על רשימות מקושרות טכניקות חיפוש מהירות, דוגמת חיפוש בינארי.
ניתן להשתמש ברשימות מקושרות כדי לנהל בלוקים של זיכרון בהם מאוחסנים קבצים. כל בלוק מחזיק את המידע ומצביע על הבלוק הבא בזכרון. דוגמה אחרת לשימוש היא בהיסטוריה של דפדפני אינטרנט. כל דף שבו ביקר המשתמש מאוחסן כאיבר ברשימה המכיל את המידע על כתובת ה-URL ומצביע על הדף הקודם. שימוש זה מאפשר למשתמש לחזור אחורה בהיסטוריית הדפים בהם גלש ידי כך שעוקבים אחר המצביעים מכל כתובת לקודמתה בזכרון.
רשימה מקושרת מורכבת מאיברים nodes כשכל איבר מצביע על האיבר הבא ברשימה, והאיבר האחרון מצביע על Null (מכונה None בפייתון).
בניגוד למערכים (מכונים list בפייתון כדי לבלבל תלמידים), הדורשים אחסון האיברים ברצף בזיכרון המחשב, איברי הרשימות המקושרות מפוזרים בזיכרון כשכל אחד מהם מצביע על מיקומו של הבא בתור. לאופן זה של ניהול נתונים יש יתרונות וחסרונות שגם אותם נסביר בהמשך המדריך.
הגדרת קלאס Node בשביל איבר ברשימה
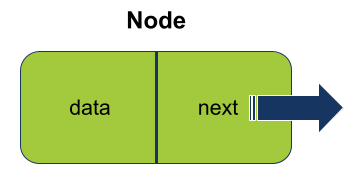
רשימה מקושרת בנויה מאיברים, Nodes. לכל איבר 2 תכונות, מידע ומצביע על האיבר הבא ברשימה:
- data - המידע שהאיבר מכיל
- next - מצביע על האיבר הבא ברשימה
class Node:
def __init__(self, data=None, next=None):
self.data = data
self.next = next
הגדרת קלאס LinkedList בשביל רשימה מקושרת
האיבר הראשון ברשימה מכונה ראש הרשימה head, ואין מצביע next אשר מצביע עליו.
אם הרשימה ריקה אז ה-head יצביע על None:
class LinkedList:
def __init__(self):
self.head = Noneאם הרשימה מכילה שני איברים אז התכונה next של הראשון תצביע על האיבר השני:
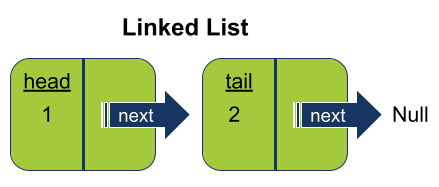
- האיבר בראש הרשימה מכונה head. האיבר בזנב הרשימה tail מצביע על Null (שזה אומר שהוא לא מצביע על מידע קיים בזיכרון).
הוספת איבר לסוף רשימה מקושרת
הוספת איבר לסוף הרשימה נעשית על ידי כיוון המצביע next של זנב הרשימה על ה-node החדש.
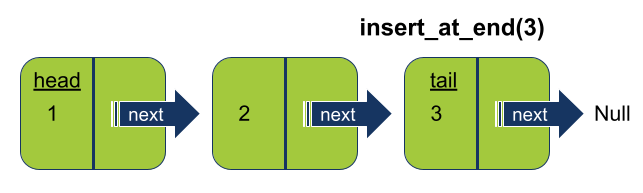
נוסיף לקלאס LinkedList את המתודה insert_at_end() אשר מוסיפה איבר לסוף הרשימה:
def insert_at_end(self, data):
new_node = Node(data)
if self.head is None:
self.head = new_node
else:
current = self.head
while current.next:
current = current.next
current.next = new_node
return node- המתודה מתחילה מיצירת איבר חדש מהקלאס Node.
- אם הרשימה ריקה המתודה תוסיף את ה-node בתור ראש הרשימה head.
- אם הרשימה אינה ריקה המתודה תעבור באופן סדרתי traverse על איברי הרשימה וכשתגיע לאיבר האחרון ברשימה תכוון את המצביע next של האיבר על ה-node החדש.
הוספת איבר לתחילת רשימה מקושרת
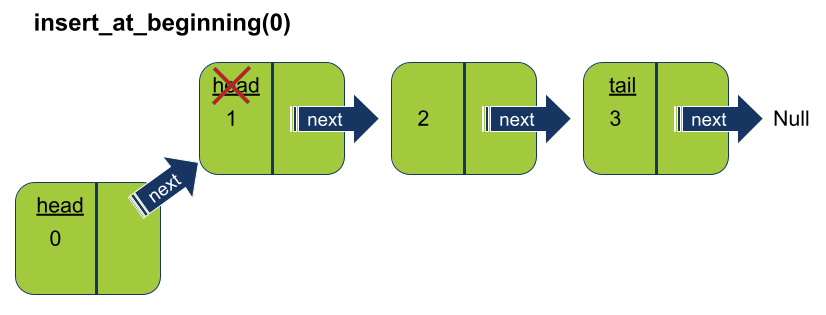
בניגוד למערך, אפשר להוסיף איבר עוד לפני ראש הרשימה הקיים על ידי כיוון next של ה-node החדש על ה-head המקורי של הרשימה וכיוון ה-head של הרשימה על האיבר החדש.
נוסיף את המתודה insert_at_beginning() שתוסיף איברים לתחילת הרשימה:
def insert_at_beginning(self, data):
new_node = Node(data)
new_node.next = self.head
self.head = new_node- המתודה מתחילה מיצירת איבר node חדש וכיוון ה-next שלו על ה-head הקיים של הרשימה.
- המתודה מסיימת בהגדרת ה-head של הרשימה על ה-node החדש.
מעבר סדרתי על איברי רשימה מקושרת traversal
כדי לעבור באופן סדרתי על איברי הרשימה traverse מתחילים מה-node בראש הרשימה. המצביע של head מצביע על האיבר השני ברשימה אז עוברים לאיבר השני ברשימה. ה-next של השני מצביע על האיבר השלישי אז עוברים אליו. וחוזר חלילה, עוברים לפי סדר על כל ה-nodes הבאים בתור באמצעות התכונה next של כל node . המעבר נפסק כשמגיעים ל-Null כיוון שזנב הרשימה למעשה לא מצביע על שום דבר. הפסאודו-קוד הבא מדגים תהליך של מעבר סדרתי באמצעות לולאה שמתקדמת בכל פעם איבר אחד:
current = head
while current:
current = current.next
נסביר:
-
current = head
המצביע pointer ששמו current מתחיל מהצבעה לראשה של הרשימה head.
-
הלולאה while תרוץ כל עוד המצביע אינו None כדי להבטיח שעוברים על כל האיברים ברשימה עד סופה.
-
בתוך הלולאה רצה השורה:
current = current.next
בשורה זו הערך של current.next מחליף את הערך של current ועל ידי זה הסמן מתקדם לאיבר הבא ברשימה.
נוסיף לקלאס LinkedList מתודה count_nodes() אשר מיישמת מעבר סדרתי על איברי הרשימה traversal לצורך ספירת מספר האיברים ברשימה:
def count_nodes(self):
count = 0
current_node = self.head
while current_node:
count += 1
current_node = current_node.next
return count- המתודה מתחילה באתחול המונה count ל-0. תפקיד המונה לעקוב אחר מספר ה-nodes ברשימה.
- הגדרת current_node על head הרשימה כדי להכין את השטח למעבר על איברי הרשימה באופן סדרתי traversal.
- כניסה ללולאה while שתמשיך לרוץ כל עוד ישנם איברים נוספים ברשימה (כל עוד current_node אינו None).
- בתוך הלולאה, תוסיף אחד למונה עבור כל איבר נוסף.
current_node = current_node.nextמניע את המעבר לאיבר הבא של הרשימה.
- חזרה על שלבים 4 ו- 5 עד שמגיעים לסוף הרשימה כאשר current_node מקבלת ערך None.
- כאשר הלולאה מסיימת לרוץ, תחזיר את הערך אותו צבר המונה count המייצג את מספר האיברים ברשימה.
מתודה להדפסת רשימה מקושרת באמצעות מעבר סדרתי
חשוב להוסיף מתודת __str__ לכל קלאס כדי להדפיס את תוצאת ההפעלה של הקלאס. (למה ואיך? קרא על מתודות ותכונות קסם של פייתון). אנחנו נשתמש במעבר סדרתי traversal בשביל להדפיס את התוצאה של הקלאס:
def __str__(self):
ll_str = ""
current_node = self.head
while current_node:
ll_str += f"{current_node.data}->"
current_node = current_node.next
ll_str += "None"
return ll_str
הסרת איבר מרשימה מקושרת
נוסיף את המתודה remove() שתפקידה להסיר nodes מהרשימה. הדבר הראשון הוא לבדוק אם הרשימה ריקה:
def remove(self, data):
if self.head is None:
return- התנאי הראשון אותו יש לבדוק הוא אם הרשימה ריקה. כלומר, האם head הוא None. במקרה זה המתודה לא תחזיר דבר.
במקרה בו צריך להסיר את האיבר הראשון של הרשימה המתודה תכוון את ה-head של ה-LinkedList על האיבר הבא של הרשימה:
def remove(self, data):
if self.head is None:
return
# If the node to remove is the head node
# point head to the next node then return
if self.head.data == data:
self.head = self.head.next
return- אם המידע data אשר ב-node הראשון של הרשימה (מכונה head) תואם לערך הפרמטר data אותו קיבלה הפונקציה יש להסיר את האיבר. לשם כך, הפונקציה תעדכן את head הרשימה להצביע על ה-next של האיבר המהווה head ברשימה הנוכחית.
self.head = self.head.nextכדי להבין איך מסירים איבר מהאמצע צריך לקחת בחשבון 3 איברים בכל פעם:
- האיבר הנוכחי
- האיבר הקודם לנוכחי
- האיבר הבא אחרי הנוכחי
במידה והאיבר אותו רוצים להסיר הוא לא האיבר הראשון יש לעבור על האיברים באופן סדרתי ואם נמצא האיבר אותו מבקשים להסיר יש לכוון את המצביע next של ה-node הקודם לנוכחי על ה-node הבא אחרי הנוכחי:
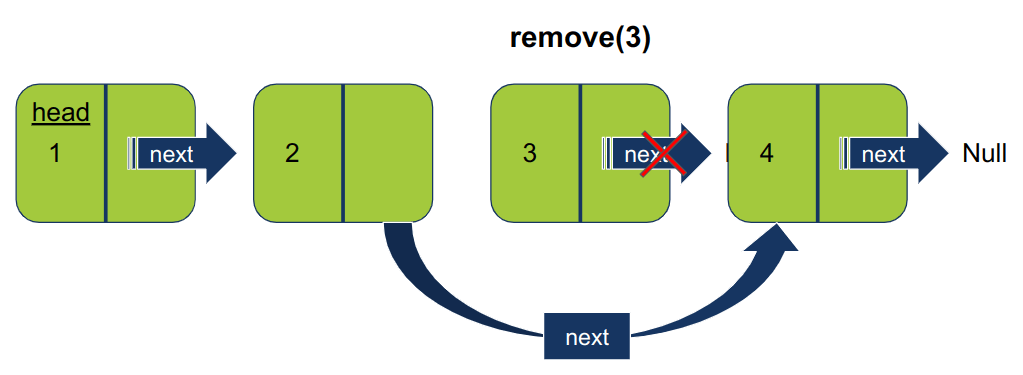
def remove(self, data):
if self.head is None:
return
# If the node to remove is the head node
# point head to the next node then return
if self.head.data == data:
self.head = self.head.next
return
# Prepare for list traversal
current_node = self.head
prev_node = None
# As long as data is not found
# store the values of the previous and next nodes
while current_node and current_node.data != data:
prev_node = current_node
current_node = current_node.next
# If not found - return
if current_node is None:
return
# If found - point previous node to next node
prev_node.next = current_node.next
ועכשיו הכל ביחד
אחרי שהסברנו וכתבנו נסכם.
קלאס Node:
class Node:
"""
A node in a linked list.
Attributes:
data: The data stored in the node.
next: The next node in the list.
"""
def __init__(self, data=None, next=None):
"""
Initialize a node with the given data and next node.
Args:
data: The data to store in the node.
next: The next node in the list.
"""
self.data = data
self.next = nextקלאס LinkedList:
class LinkedList:
"""
A linked list.
Attributes:
head: The head node of the list.
"""
def __init__(self):
"""
Initialize an empty linked list.
"""
self.head = None
def insert_at_end(self, data):
"""
Append the given data to the end of the list.
Args:
data: The data to append to the list.
"""
new_node = Node(data)
if self.head is None:
self.head = new_node
else:
current_node = self.head
while current_node.next:
current_node = current_node.next
current_node.next = new_node
def insert_at_beginning(self, data):
"""
Insert the given data at the beginning of the list.
Args:
data: The data to insert at the beginning of the list.
"""
new_node = Node(data)
new_node.next = self.head
self.head = new_node
def remove(self, data):
"""
Remove the node with the given data from the list.
Args:
data: The data of the node to remove.
"""
if self.head is None:
return
# If the node to remove is the head node
# point head to the next node then return
if self.head.data == data:
self.head = self.head.next
return
# Prepare for list traversal
current_node = self.head
prev_node = None
# As long as data is not found
# store the values of the previous and next nodes
while current_node and current_node.data != data:
prev_node = current_node
current_node = current_node.next
# If not found - return
if current_node is None:
return
# If found - point previous node to next node
prev_node.next = current_node.next
def count_nodes(self):
"""
Count the number of nodes in the linked list.
Returns:
The number of nodes in the linked list.
"""
count = 0
current_node = self.head
while current_node:
count += 1
current_node = current_node.next
return count
def __str__(self):
"""
Return a string representation of the list.
Returns:
A string representation of the list.
"""
ll_str = ""
current_node = self.head
while current_node:
ll_str += f"{current_node.data}->"
current_node = current_node.next
ll_str += "None"
return ll_str
ניתוח ביצועים
כפי שראינו, רשימה מקושרת linked list היא שרשרת של איברים nodes, כאשר כל איבר מכיל מידע data ומצביע next שמורה על האיבר הבא בשרשרת. העובדה שמבנה הנתונים נעזר במצביע מקלה על אחסון הנתונים כי לא צריך לשנות את הגודל המוקצה בזכרון (כמו שצריך לעשות עם מערכים) מה שאומר שאם רוצים להוסיף או להסיר איבר מראש הרשימה או מסופה אז משך הזמן לביצוע מוערך כזמן קבוע O(1) מה שהופך את הפעולות להכי יעילות שאפשר (אם משהו לא ברור נא לקרוא את מדריך big - O). מצד שני, גישה לאיברים, תוספת או מחיקה מאמצע הרשימה דורש מעבר סדרתי traversal שמשך הזמן שלו במקרה הגרוע הוא לינארי O(n).
"המתחרה" העיקרי של רשימות מקושרות הוא המערך. מערכים של פייתון מציעים יתרון בביצועים כשרוצים לגשת או לערוך פריטים באמצע המערך בגלל שניתן לגשת לפריטים על סמך האינדקס שלהם. מחיקה או הוספה של פריטים לאמצע המערך היא מסובכת יותר מאשר ב-linked list בגלל שצריך להזיז את כל הפריטים אחרי מקום השינוי. כיוון שמערכים ורשימות מקושרות מציעים יתרונות וחסרונות שונים צריך לבחור במבנה על פי הנדרש במשימה התכנותית. בדרך כלל הנטייה היא לבחור במערכים אבל ידע על רשימות מקושרות עשוי להועיל עבור משימות ספציפיות.
אתגרים תכנותיים עבור רשימות מקושרות
אתגר 1: זיהוי כפילויות ברשימה מקושרת
עליך לכתוב פונקציה שמקבלת רשימה מקושרת בתור קלט ומחזירה True אם הרשימה מכילה ערכים כפולים, אחרת False. לשם כך, עליך ליישם את הפונקציה detect_duplicates(head) כאשר head הוא האיבר הראשון של הרשימה המקושרת.
לדוגמה, אם מעבירים לפונקציה את הרשימה המקושרת:
1 -> 2 -> 3 -> 2 -> 4
הפונקציה צריכה להחזיר True כיוון שה-node שערכו 2 מופיע פעמיים ברשימה.
דוגמה נוספת, אם מעבירים לפונקציה את הרשימה המקושרת:
5 -> 7 -> 9 -> 3 -> 1
הפונקציה צריכה להחזיר False כיוון שאין כפילויות ברשימה.
תנסה לכתוב פונקציה:
detect_duplicate(head: Node) -> boolשמקבלת את ה-head של רשימה כפרמטר.
רק אחרי שניסית אתה רשאי להציץ בפתרון. אם תציץ בלי לנסות אז דיר-באלק! אני לא אחראי לתוצאה…
תשובה לדוגמה:
# Take the head node of the linked list as an input
def detect_duplicates(head):
# Initialize an empty list, elements, to keep track of elements encountered.
current = head
elements = []
# Iterate through the linked list by traversing the nodes using the next pointers.
while current:
# For each node, check if the data value is already present in the elements list.
# If a duplicate is found, return True.
if current.data in elements:
return True
# Append the current node to the elements list
elements.append(current.data)
current = current.next
# If the end of the linked list is reached without finding any duplicates return False
return Falseנבחן את הפתרון:
# Case 1: Has no duplicate
l = [1, 2, 3]
ll = LinkedList()
for item in l:
ll.insert_at_end(item)
print(detect_duplicates(ll.head)) # False
# Case 2: Contains duplicate
l = [1, 2, 3, 1]
ll = LinkedList()
for item in l:
ll.insert_at_end(item)
print(detect_duplicates(ll.head)) # True
אתגר 2: זיהוי מעגל ברשימה מקושרת
נותנים לך רשימה מקושרת ואתה צריך לבדוק האם היא מכילה מעגל.
def has_cycle(head: Node) -> bool:
pass- Input: הפונקציה has_cycle מקבלת את ה-head של רשימה מקושרת בתור קלט.
- Output: הפונקציה צריכה להחזיר ערך בוליאני- True אם הפונקציה מכילה מעגל. אחרת False.
דוגמאות:
דוגמה 1:
קלט:
head = 1 -> 2 -> 3 -> 1פלט:
Trueהסבר:
הרשימה המקושרת מכילה מעגל: הצומת שערכו 3 מצביע חזרה על הצומת שערכו 1.
דוגמה 2:
קלט:
head = 1 -> 2 -> 3פלט:
Falseהאתגר הוא ליישם את הפונקציה has_cycle לבדיקה האם רשימה מקושרת מכילה מעגל. אם מעגל קיים הפונקציה צריכה להחזיר True אחרת False.
פתרון:
לפני שנוכל למצוא את הפתרון אנחנו צריכים שתהיה לנו דרך לגרום לזנב להצביע על אחד הצמתים ברשימה המקושרת. לשם כך, נגדיר את המצביע next.
לדוגמה, נתונה רשימה שבה הזנב מצביע על הראש כי שניהם אותו node שהוא 1:
1 -> 2 -> 3 -> 1
בשביל ליצור את הרשימה, נגדיר בקוד שהזנב 3 יצביע על 1:
ll = LinkedList()
n1 = ll.insert_at_end(1)
n2 = ll.insert_at_end(2)
n3 = ll.insert_at_end(3)
n3.next = n1
הפתרון מסתמך על אלגוריתם שחשוב לדעת המכונה Floyd algorithm או "אלגוריתם הצב והארנב" שבו משתמשים ב- 2 מצביעים. אחד מהיר שרץ פי 2 יותר מהר מהאיטי:
fast = fast.next.next slow = slow.next
אם קיים מעגל ברשימה המקושרת, המצביע המהיר יפגע באיטי באיזשהו שלב מה שיגרום לקיום השוויון:
fast == slow
אחרת, המצביע המהיר מגיע לזנבה של הרשימה המקושרת.
פתרון לדוגמה כולל בדיקות קוד:
def has_cycle(head):
# Initialize slow and fast pointers to the head of the linked list
slow, fast = head, head
while fast and fast.next:
# Move the slow pointer one step at a time
slow = slow.next
# Move the fast pointer two steps at a time
fast = fast.next.next
# If there is a cycle, the fast pointer will eventually catch up with the slow pointer
if fast == slow:
return True
# If the fast pointer reaches the end (null) or the next node (null), there is no cycle
return False
# Test cases
ll = LinkedList()
ll.insert_at_end(1)
ll.insert_at_end(2)
ll.insert_at_end(3)
print(ll)
res = has_cycle(ll.head)
print(res)
# Output: False
ll1 = LinkedList()
n1 = ll1.insert_at_end(1)
n2 = ll1.insert_at_end(2)
n3 = ll1.insert_at_end(3)
n3.next = n1
# The linked list cannot be printed because it has a cycle
res = has_cycle(ll1.head)
print(res)
# Output: Trueהסברנו את הקוד אבל למה הוא עובד?
נדגים באמצעות רשימה מקושרת שבה הזנב "3" מצביע על ראש הרשימה "0":
0 -> 1 -> 2 -> 3 -> 0
שני המצביעים, fast ו-slow מתחילים מפוזיציה "0". אחרי פעם אחת שהלולאה רצה האיטי נמצא בפוזיציה "1" והמהיר בפוזיציה "2". בפעם השנייה שהלולאה רצה האיטי יתקדם בצעד 1 לפוזיציה "2" והמהיר יתקדם שני צעדים ויחזור לפוזיציה "0".
וחוזר חלילה עד שייפגשו. נסכם את הפוזיציות שבהם המצביעים נמצאים באמצעות טבלה:
| iteration | slow | fast |
|---|---|---|
| 1 | 1 | 2 |
| 2 | 2 | 0 |
| 3 | 3 | 2 |
| 4 | 0 | 0 |
4 צעדים דרושים כדי לגרום למצביעים האיטי והמהיר להיפגש באותה הפוזיציה וזה גם אורך הלולאה. זה היה עובד גם עבור לולאה באורך 5, 6 וכיו"ב אז על סמך אינדוקציה אנחנו יכולים להסיק שדרושים n צעדים כדי לאתר לולאה אם משתמשים באלגוריתם "הארנב והצב" המשתמש בשני סמנים - איטי שנע צעד אחד בכל פעם ומהיר שנע פי 2 מהר יותר.
אתגר 3: היפוך רשימה מקושרת
נתונה לך התחלה של קוד הפונקציה ששמה reverse_linked_list() שמקבלת קלט head של רשימה מקושרת ומחזירה רשימה מקושרת שבה סדר האיברים הפוך. עליך להשלים את הקוד החסר:
def reverse_linked_list(head: Node) -> Node:
...נראה 3 דוגמאות לקלט ופלט הפונקציה.
-
בהינתן רשימה:
1 -> 2 -> 3 -> 4 -> 5
הפונקציה צריכה להחזיר את הרשימה בסדר הפוך:
5 -> 4 -> 3 -> 2 -> 1
-
בהינתן רשימה:
1
הפונקציה צריכה להחזיר:
1
- בהינתן רשימה ריקה הפונקציה תחזיר רשימה ריקה.
הפתרון משתמש בשני מצביעים:
-
prev: מצביע העוקב אחר הצומת הקודם ברשימה כיוון שאין לנו מצביע על האיבר הקודם ברשימה מקושרת אנחנו צריכים משתנה שיאפשר לנו לדעת מיהו האיבר הקודם.
-
current: מצביע על הצומת הנוכחי ברשימה המקושרת.
שני המצביעים עובדים יחד כדי להפוך את הרשימה המקושרת במקום. כאשר מצביע prev מורה על האיבר הבא ברשימה ההפוכה, בעוד שמצביע curr מתקדם בתוך הרשימה המקורית. השילוב של שניהם בקוד גורם לכל איבר ברשימה ההפוכה להצביע על האיבר הקודם במקום על הבא.
אנחנו יכולים ליצור רשימה חדשה אבל זה פתרון פחות יעיל. הפתרון שלנו מבוסס על היפוך מצביעי next של כל איבר בתוך רשימה קיימת. משך הזמן הדרוש לביצוע המשימה הוא יעיל O(n) כיוון שצריך לעבור על כל איבר ברשימה שאורכה n בדיוק פעם אחת והמקום בזכרון הנדרש לפעולה הוא קבוע O(1) כיוון שגישת הפתרון מבוססת הלולאה אותה נציג מיד אינה דורשת תוספת זיכרון לצורך הפתרון כיוון שכל השינויים נעשים במקום, על ידי מניפולציה של מצביעים, ללא צורך במבני נתונים נוספים.
הקוד להלן פותר את הבעיה של היפוך הרשימה המקושרת:
def reverse_linked_list(head: Node) -> Node:
# Initialize pointers:
# `prev` - Keeps track of the previous node
# `curr` - Keeps track of the current node
prev = None
curr = head
# Keep iterating while the `curr` pointer hasn't reached the tail of the original list
while curr:
# Cache the pointer to the next node
next = curr.next
# Reverse the `next` pointer of the current node to point to the previous node
curr.next = prev
# Advance `prev` pointer to the current position
prev = curr
# Advance `curr` pointer to the next node in the original list
curr = next
# Return the head of the reversed list
return prev
# Test cases
# Test case 1: Reverse a multi-node linked list
ll1 = LinkedList()
ll1.append(1)
ll1.append(2)
ll1.append(3)
ll1.append(4)
ll1.head = reverse_linked_list(ll1.head)
ll1.display()
# Output: 4 -> 3 -> 2 -> 1 -> None
# Test case 2: Reverse a single-node linked list
ll2 = LinkedList()
ll2.append(1)
ll2.head = reverse_linked_list(ll2.head)
ll2.display()
# Output: 1 -> Noneנסביר:
המטרה היא לסובב את כיוונו של כל איבר ברשימה כך שהמצביע next של כל איבר יצביע על האיבר הקודם במקום על הבא בתור.
פתרון האתגר משתמש בשני מצביעים (Two pointers):
- curr - מצביע על האיבר הנוכחי
- prev - מצביע על האיבר הקודם
-
נאתחל את שני המצביעים:
curr = head prev = None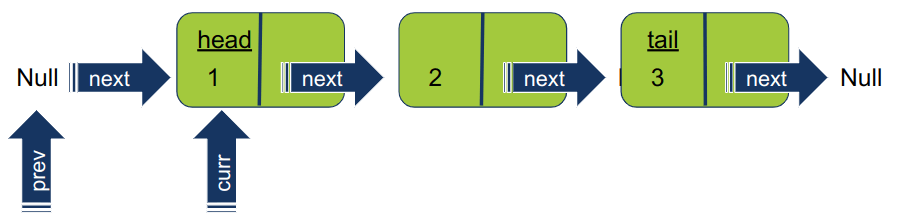
- המצביע curr מצביע על ראש הרשימה ממנו מתחילים לסרוק את הרשימה.
המצביע prev מורה מאותחל להיות None (=אין מקום כזה בזכרון, Null) כי אין איבר המקדים את ראש הרשימה. המעקב אחר מיקומו של האיבר הקודם הוא חשוב כדי שנדע להיכן להפנות את המצביע next לאחר ההיפוך.
במסגרת ההיפוך, המצביע curr עובר להצביע על האיבר הקודם עליו מצביע prev. כך יוצא שהמצביע עובר להצביע על Null והופך את האיבר הראשון ברשימה לזנב של רשימה.
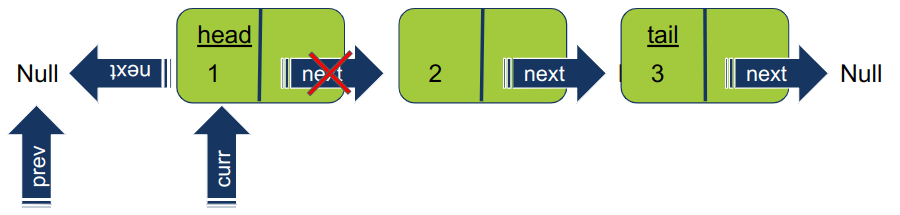
-
מזיזים את המצביעים prev ו- curr כל אחד בנפרד איבר אחד קדימה ברשימה המקורית. עכשיו prev מצביע על איבר 1 ו- curr על 2.
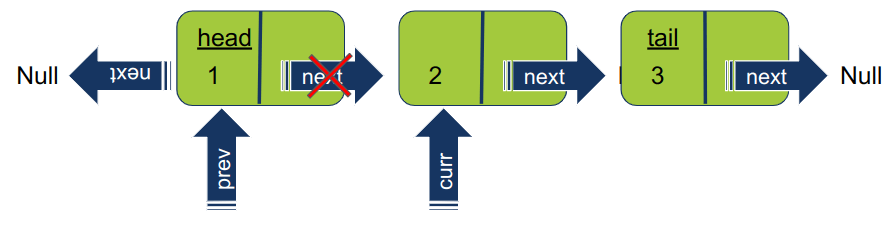
עדיין באותו שלב. מסובבים את המצביע של האיבר עליו מצביע curr כדי שיצביע על האיבר הקודם prev. במקום בו אנו נמצאים בתהליך, האיבר 2 יעבור להצביע על 1.
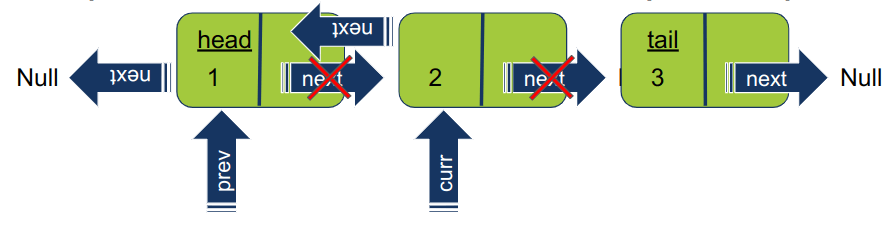
-
חוזרים על אותו התהליך גם עבור האיבר הבא ברשימה. מזיזים את המצביעים curr ו-prev איבר אחד קדימה, ואז מפנים את המצביע של האיבר הנוכחי על האיבר הקודם. במקרה שלנו, איבר 3 עובר להצביע על 2.
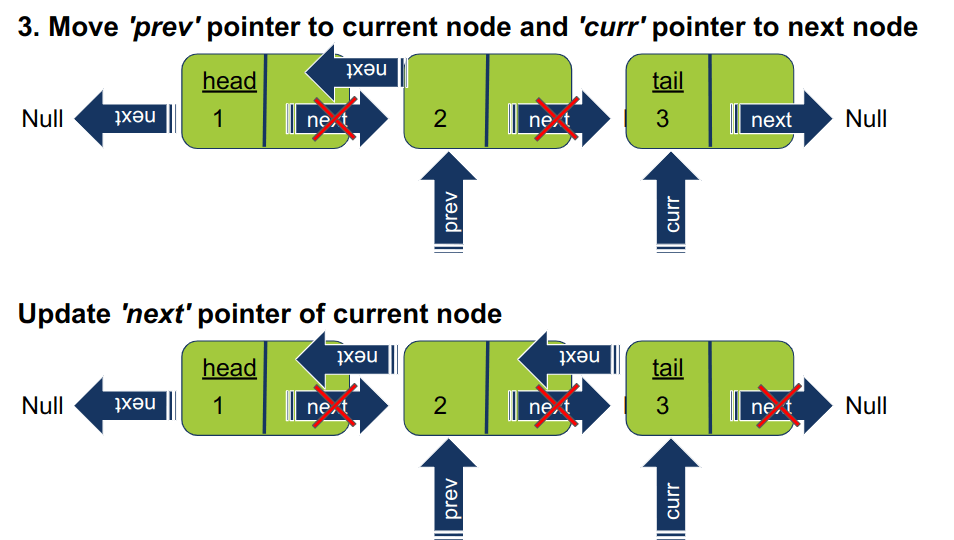
-
התהליך חוזר על עצמו גם כשמגיעים לאיבר האחרון ברשימה. מעבר לאיבר האחרון נמצא Null כשהמצביע curr מתקדם צעד נוסף הוא מקבל ערך Null דבר המסיים את האיטרציה.
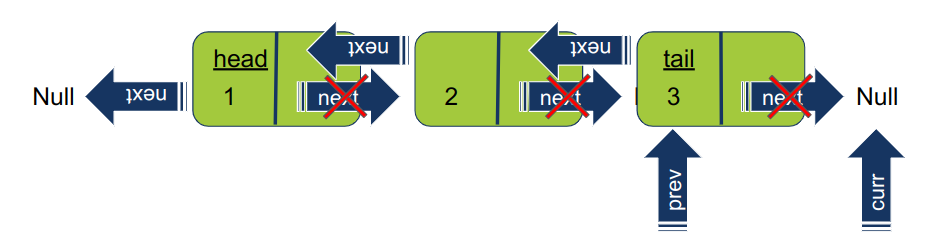
-
בשלב האחרון, מחזירים את ה-head של הרשימה ההפוכה.
אתגר 4: פיצול רשימה מקושרת
עליך לפצל רשימה מקושרת לשתי רשימות מקושרות נפרדות - אחת שמקורה בחצי הקדמי של הרשימה המקורית ושנייה שמקורה החצי האחורי. אם מספר האיברים ברשימה המקורית אינו זוגי, האיבר הנוסף צריך להשתייך לחצי הקדמי. הפתרון צריך להיות במסגרת של פונקציה: split_in_two(head) אשר מקבלת פרמטר head של הרשימה אותה רוצים לפצל ומחזירה את שני הראשים של הרשימות שנוצרו בעקבות הפיצול.
def split_in_two(head: Optional[Node]) -> Tuple[Optional[Node], Optional[Node]]:
....- קלט: ראש הרשימה המקושרת שיכול להיות Node או None (במקרה של רשימה ריקה).
- פלט: טאפל של פייתון. המכיל שני heads - הראשון עבור הרשימה שמקורה בחציו הראשון של הרשימה המקורית, ושני שמקורו בחצי השני.
דוגמאות:
קלט: רשימה מקושרת בעלת מספר אי זוגי של איברים:
1 -> 2 -> 3 -> 4 -> 5
פלט: 2 רשימות מקושרות:
1 -> 2 -> 3, 4 -> 5
קלט: רשימה מקושרת בעלת מספר זוגי של איברים:
1 -> 2 -> 3 -> 4
פלט: 2 רשימות מקושרות:
1 -> 2 , 3 -> 4
קלט: רשימה מקושרת ריקה.
פלט:
None , None
קלט: רשימה מקושרת בעלת איבר בודד: 1
פלט:
1 , None
פתרון לדוגמה:
def split_in_two(head):
# Check if the linked list is empty or has only one node
if not head or not head.next:
return head, None
# Initialize two pointers: fast and slow
fast = head.next
slow = head
# Move the fast pointer twice as fast as the slow pointer
while fast and fast.next:
fast = fast.next.next
slow = slow.next
# Split the linked list into two halves
# Head of the second half
second_half_head = slow.next
# Set the next of slow pointer to None to separate the halves
slow.next = None
# Head of the first half
first_half_head = head
# return tuple with the heads of the two lists
return first_half_head, second_half_head
ll = LinkedList()
ll.insert_at_end(1)
ll.insert_at_end(2)
ll.insert_at_end(3)
ll.insert_at_end(4)
ll.insert_at_end(5)
# Split the linked list into two halves
first_head, second_head = split_in_two(ll.head)
# Create a new linked list for the two halves
first_half_linked_list = LinkedList()
first_half_linked_list.head = first_head
second_half_linked_list = LinkedList()
second_half_linked_list.head = second_head
# Print the two halves
print(first_half_linked_list)
print(second_half_linked_list)נסביר:
- הפונקציה split_in_two מקבלת head של רשימה מקושרת כקלט.
- קודם כל היא בודקת אם הרשימה המקושרת היא ריקה או שיש לה איבר אחד בלבד. אם זה המצב, היא תחזיר את ה- head של הרשימה בתור החלק הראשון ו-None בתור החלק השני.
- היא מיישמת דפוס שחייבים לדעת "אלגוריתם הצב והארנב" אשר משתמש בשני מצביעים slow ו-fast אותם היא מקדמת לאורך הרשימה. את המצביע fast מזיזים כפליים יותר מהר מאשר את המצביע slow וכך קורה כי כאשר fast מסיים לרוץ כי הוא הגיע לסוף הרשימה, slow נמצא באיבר האמצעי מה שהופך את האלגוריתם לשימושי ביותר כשרוצים לעשות משהו עם אמצע של רשימה.
- הפונקציה מפצלת את הרשימה באמצעות עדכון המצביע slow.next כך שיצביע על None.
אתגר 5: מיזוג שתי רשימות מקושרות
נתונות שתי רשימות מקושרות, l1 ו-l2 כל אחת מהם מסודרת בסדר עולה. עליך למזג את שתי הרשימות לרשימה מקושרת אחת ולהחזיר את ראשה של הרשימה הממוזגת. הרשימה צריכה להיות בסדר עולה.
עליך לכתוב פונקציה merge_lists כדי לפתור את האתגר:
def merge_lists(l1: Node, l2: Node) -> Node:
...דוגמאות:
בהינתן 2 רשימות מקושרות:
l1: 1 -> 2 -> 6
l2: 1 -> 3 -> 4 -> 5
הפונקציה תחזיר רשימה ממוזגת:
1 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6
פתרון:
def merge_lists(l1, l2):
# A new linked list to store the merged list
merged = LinkedList()
# Pointers to traverse the lists: l1 and l2
current1 = l1.head
current2 = l2.head
# Merge the two lists in sorted order
while current1 and current2:
if current1.data <= current2.data:
# If current1 data is smaller, insert it into the merged list
merged.insert_at_end(current1.data)
current1 = current1.next
else:
# If current2 data is smaller, insert it into the merged list
merged.insert_at_end(current2.data)
current2 = current2.next
# Append the remaining nodes from either l1 or l2
while current1:
merged.insert_at_end(current1.data)
current1 = current1.next
while current2:
merged.insert_at_end(current2.data)
current2 = current2.next
return merged
# Test case
l1 = LinkedList()
l1.insert_at_end(1)
l1.insert_at_end(2)
l1.insert_at_end(6)
l2 = LinkedList()
l2.insert_at_end(1)
l2.insert_at_end(3)
l2.insert_at_end(4)
l2.insert_at_end(5)
# Merge the two lists
merged_list = merge_lists(l1, l2)
# Print the merged list
print(merged_list)נסביר:
-
merged = LinkedList()יוצרים אובייקט חדש LinkedList שיאחסן את הרשימה הממוזגת.
-
current1 = l1.head current2 = l2.headאתחול שני מצביעים current1 ו-current2 שיצביעו על ראשי הרשימות l1 ו-l2. מצביעים אילה יעברו באופן סדרתי traverse על שתי הרשימות.
-
while current1 and current2: if current1.data <= current2.data: merged.insert_at_end(current1.data) current1 = current1.next else: merged.insert_at_end(current2.data) current2 = current2.next- נכנסים ללולאה שתמשיך לרוץ כל עוד current1 ו-current2 אינם None.
- בתוך הלולאה משווים בין הערכים של
current1
ו-current2.
- אם הערך של current1 הוא נמוך או שווה ל-current2, מכניסים את האיבר עליו מצביע current1 לרשימה הממוזגת, ומזיזים את הסמן current1 לאיבר הבא בתור.
- אחרת, מכניסים את הערך של current2 לרשימה הממוזגת
-
# Append the remaining nodes from either l1 or l2 while current1: merged.insert_at_end(current1.data) current1 = current1.next while current2: merged.insert_at_end(current2.data) current2 = current2.nextאחרי שהלולאה מסיימת לרוץ יתכנו איברים נוספים שלא עברנו עליהם ב-l1 או l2, אז עוברים באופן סדרתי על האיברים הנותרים ומוסיפים את ערכם לרשימה merged.
לסיכום
רשימות מקושרות Linked lists הם מבנה נתונים שצריך להכיר בגלל שהוא מאפשר גמישות באחסון ובמניפולציה של מידע. בניגוד למערכים רשימות מקושרות מקצות זיכרון באופן דינמי לכל איבר בנפרד, מה שמאפשר הוספה ומחיקה של איברים ביעילות רבה. במדריך הסברנו את העקרונות של רשימות מקושרות, החל במבנה. כל איבר node מכיל מידע ומצביע לאיבר הבא. הקלאס LinkedList מכיל בתוכו את האופרציות החשובות ביותר לניהול רשימות מקושרות, כדוגמת: הוספה לסוף הרשימה, מעבר סדרתי ומחיקה.
בחלק האתגרים הדגמנו מספר אופרציות המהוות כישורים הכרחיים לכל מי שצריך לעבוד עם רשימות מקושרות או לעבור רעיון טכני. בין השאר, למדנו כיצד להפוך רשימה, למזג, ולפצל. בפתירת האתגרים שמנו דגש על רעיונות לפתרון בעיות תכנותיות, דוגמת השימוש בשני מצביעים, ו-"אלגוריתם הצב והארנב".
לסיכום, רשימות מקושרות הם מבנה נתונים שצריך לדעת. יש להם מאפיינים ופונקציונליות הנובעים ממאפינים אילה ויתרונות וחסרונות ביחס למבני נתונים דוגמת מערך. אני מאוד מקווה שמדריך זה הקנה לך תובנות וכלים אודות linked lists שיאפשרו לך למנף את כוחם לפתרון בעיות תכנותיות באופן אפקטיבי.
מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך
יישום תורת הגרפים בפייתון - חלק א
מה זה data classes בפייתון ואיך להשתמש בזה
לכל המדריכים בסדרה ללימוד פייתון
אהבתם? לא אהבתם? דרגו!
0 הצבעות, ממוצע 0 מתוך 5 כוכבים


המדריכים באתר עוסקים בנושאי תכנות ופיתוח אישי. הקוד שמוצג משמש להדגמה ולצרכי לימוד. התוכן והקוד המוצגים באתר נבדקו בקפידה ונמצאו תקינים. אבל ייתכן ששימוש במערכות שונות, דוגמת דפדפן או מערכת הפעלה שונה ולאור השינויים הטכנולוגיים התכופים בעולם שבו אנו חיים יגרום לתוצאות שונות מהמצופה. בכל מקרה, אין בעל האתר נושא באחריות לכל שיבוש או שימוש לא אחראי בתכנים הלימודיים באתר.
למרות האמור לעיל, ומתוך רצון טוב, אם נתקלת בקשיים ביישום הקוד באתר מפאת מה שנראה לך כשגיאה או כחוסר עקביות נא להשאיר תגובה עם פירוט הבעיה באזור התגובות בתחתית המדריכים. זה יכול לעזור למשתמשים אחרים שנתקלו באותה בעיה ואם אני רואה שהבעיה עקרונית אני עשוי לערוך התאמה במדריך או להסיר אותו כדי להימנע מהטעיית הציבור.
שימו לב! הסקריפטים במדריכים מיועדים למטרות לימוד בלבד. כשאתם עובדים על הפרויקטים שלכם אתם צריכים להשתמש בספריות וסביבות פיתוח מוכחות, מהירות ובטוחות.
המשתמש באתר צריך להיות מודע לכך שאם וכאשר הוא מפתח קוד בשביל פרויקט הוא חייב לשים לב ולהשתמש בסביבת הפיתוח המתאימה ביותר, הבטוחה ביותר, היעילה ביותר וכמובן שהוא צריך לבדוק את הקוד בהיבטים של יעילות ואבטחה. מי אמר שלהיות מפתח זו עבודה קלה ?
השימוש שלך באתר מהווה ראייה להסכמתך עם הכללים והתקנות שנוסחו בהסכם תנאי השימוש.