להבין את מיון מיזוג - merge sort - אלגוריתם הפרד ומשול יעיל

מיון הוא פעולה בסיסית בעולם המחשוב. ישנם אלגוריתמי מיון רבים ושונים. במדריך הזה, נלמד על אחד מתהליכי המיון הפופולריים והיעילים ביותר: מיון מיזוג merge sort.

אלגוריתם מיון מיזוג מבוסס על גישת "הפרד ומשול" divide and conquer שמפצלת בעיה גדולה לבעיות משנה שקל יותר לפתור. אם בעיות המשנה הם לא מספיק קלות לפתרון מפצלים גם אותם. וחוזר חלילה עד שמגיעים לבעיות שקל לפתור. האלגוריתם פותר את בעיות המשנה שקל לפתור, וממזג את הפתרונות חזרה לפתרון הבעיה הגדולה. מיון מיזוג מפריד את הרשימה הגדולה אותה צריך למיין לרשימות קטנות יותר ויותר עד שהן ניתנות למיון טריוויאלי. אחר כך, האלגוריתם מאחד את תת-הרשימות לרשימה אחת גדולה ממוינת.

מדריך זה יסביר את עקרונות האלגוריתם, יציג קוד פייתון ליישומו, וידון בסיבוכיות הזמן של הפתרון.

בסוף המדריך תהיה לך הבנה טובה יותר של אלגוריתם מיון מיזוג merge sort וכיצד להשתמש בו למיון יעיל של נתונים.

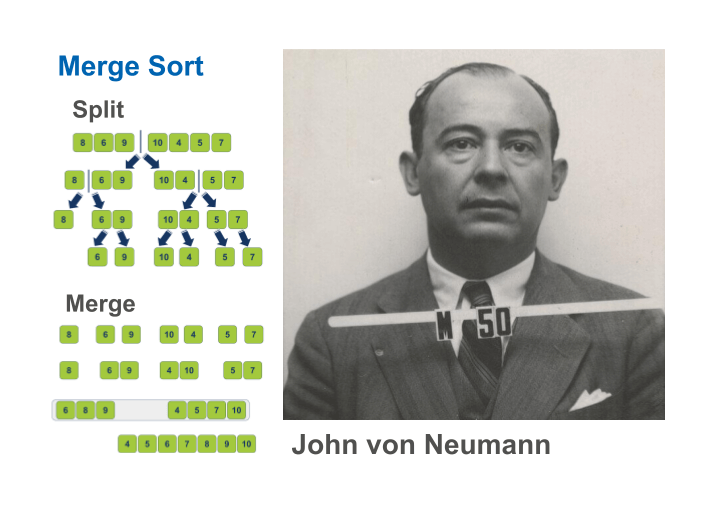
הצורך למיין ולסדר מלווה את התפתחות המחשבים עוד מראשית המצאתם. בשנות ה-1930 פיתחה חברת IBM מכונות למיזוג 2 חבילות כרטיסים לחבילה 1. המיזוג עבד מצוין כל עוד שתי החבילות היו ממוינות. תהליך המיזוג לערמה ממוינת אחת היה פשוט: השוואה בין שני הכרטיסים העליונים בכל חבילה והעברת הכרטיס בעל הערך הנמוך יותר לערמה הממוינת. חוזרים על התהליך עבור כל כרטיס בכל אחת משתי הערמות, וכשמסיימים מקבלים חבילה אחת ממוינת.

המתמטיקאי האגדי ג'ון פון נוימן פיתח את האלגוריתם מיון מיזוג בשנות ה-1940. הוא חשב על ערימה של קלפים שאותה צריך למיין. זה מאוד קשה אבל ממש קל למיין 2 קלפים אם מסדרים בשתי ערימות. בכל ערימה קלף אחד. אם אתה רוצה למזג אותם לערימה אחת מסודרת אתה רק צריך לשים את הקלף שערכו נמוך מעל לקלף שערכו גבוה. עכשיו יש לך ערימה של 2 קלפים ממוינים. בשלב זה, תשווה לערימה נוספת ממויינת שגם בה יש 2 קלפים ממוינים. תשווה את הקלף מראש הערימה הראשונה עם הקלף מראש הערימה השנייה ותעביר את הקלף הנמוך לערימה הממוינת. תחזור על התהליך עד שתסיים לעבור על כל הקלפים משתי הערימות. עכשיו יש לך ערימה של 4 קלפים ממוינים. תשווה אותה לערימה נוספת של 4 קלפים ממוינים. אחרי המיזוג שלהם תהיה לך ערימה של 8 קלפים ממוינים. אח"כ תשווה שתי ערימות של 8 קלפים ממוינים. וחוזר חלילה. בכל שלב תשווה ערימות המכילות מספר כפול של פריטים. כל שלב מכפיל פי 2 את מספר הקלפים הממוינים: בשביל לסדר 2 קלפים אתה צריך להשוות פעם 1, בשביל לסדר 4 קלפים אתה צריך להשוות פעמיים, בשביל 8 פריטים אתה צריך 3 השוואות. כלומר, כדי למיין N פריטים אתה צריך לחזור על פעולת המיון 2 בחזקת X פעמים השווה N. מה שאומר סיבוכיות זמן לוגריתמית של התהליך.

מובן מאליו שערימה שמכילה קלף 1 בודד היא ממוינת. זה המקרה הטריוויאלי. יתרה מכך, קל לסדר ולמזג 2 ערימות קלפים שבכל אחת קלף 1 לערימה אחת ממוינת המכילה 2 קלפים. חוזרים על התהליך כמה שצריך. בכל שלב ממזגים פי 2 יותר קלפים. אבל איך מקבלים מערימה אחת גדולה ערימות של קלפים בודדים? בשביל זה צריך לפצל את הערימה. מתחילים מפיצול הערימה לשני חצאים שווים. כל חצי מפצלים שוב לחצאים, וכך מקבלים 4 רבעים של הערימה המקורית, וחוזר חלילה עד שמקבלים מספר ערימות של קלפים יחידים כמספר הקלפים שהיו קיימים בערימה המקורית. בשלב זה כל ערימה המכילה קלף בודד היא ממוינת בפני עצמה. עכשיו שיש לנו ערימות של קלפים יחידים ממוינים משווים וממזגים בין זוגות של ערימות ממוינות כל ערימה מכילה קלף אחד. מקבלים ערימות של 2 קלפים ממוינים, שאותם ממזגים לערימות של 4, וחוזר חלילה, ערימות הולכות וגדלות, עד לקבלת ערימה שלמה גדולה וממוינת.

האלגוריתם משתמש בטכניקה מאוד חשובה המכונה "הפרד ומשול" divide and conquer במסגרתה מפרקים בעיה מורכבת לתת בעיות קטנות, פותרים כל אחת מתת הבעיות בנפרד, ואז משלבים את הפתרונות הקטנים לפתרון הבעיה הגדולה. האלגוריתם מיון מיזוג מחלק את רשימות הפריטים שאינם ממוינים באופן רקורסיבי לרשימות הולכות וקטנות. את הרשימות הקטנות הוא ממין וממזג חזרה ליצירת רשימה ממוינת.

אלגוריתם מיון מיזוג כולל 2 צעדים:

1. פיצול split - את הרשימה הלא ממוינת מפצלים שוב ושוב לחצאים עד שכל תת רשימה מכילה פריט אחד או אפס פריטים. תת רשימות המכילות פריט אחד או ריקות נחשבות ממוינות.
2. מיזוג merge - תת הרשימות הממוינות ממוזגות יחדיו, תוך סידור הפריטים ויצירת רשימה אחת ממוינת.

איך עובד מיון מיזוג - בסבלנות שלב אחר שלב

א. שלב החלוקה (=פיצול)

נעביר לאלגוריתם את רשימת הפריטים הבאה לצורך סידור:

האלגוריתם יחלק את הרשימה ל-2 תת רשימות שוות גודל:

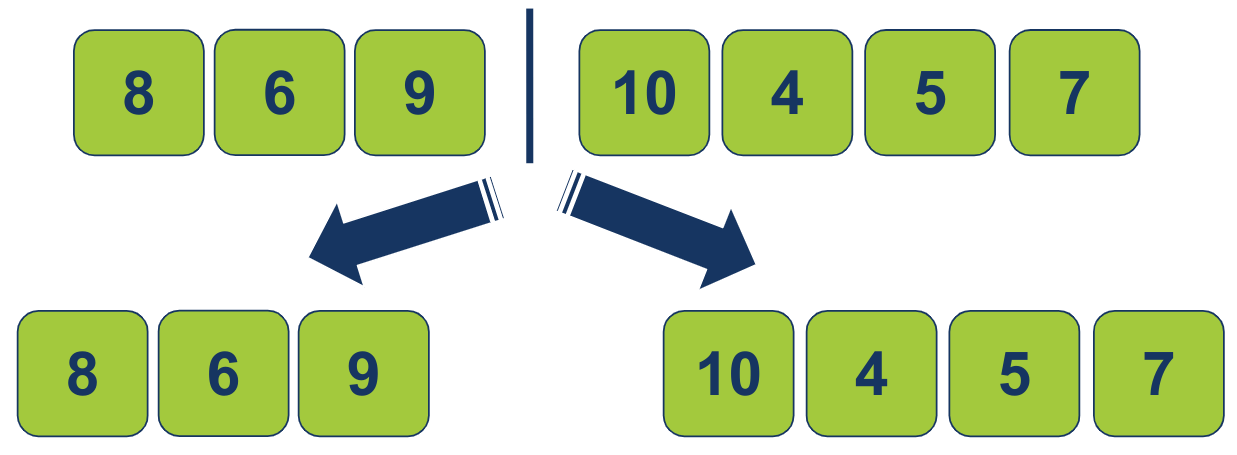
• כיוון שהרשימה מונה מספר אי זוגי של פריטים החלוקה היא לשתי תת רשימות שיש ביניהם הבדל של פריט 1. רשימה ימנית המונה 4 פריטים ושמאלית המונה שלושה.

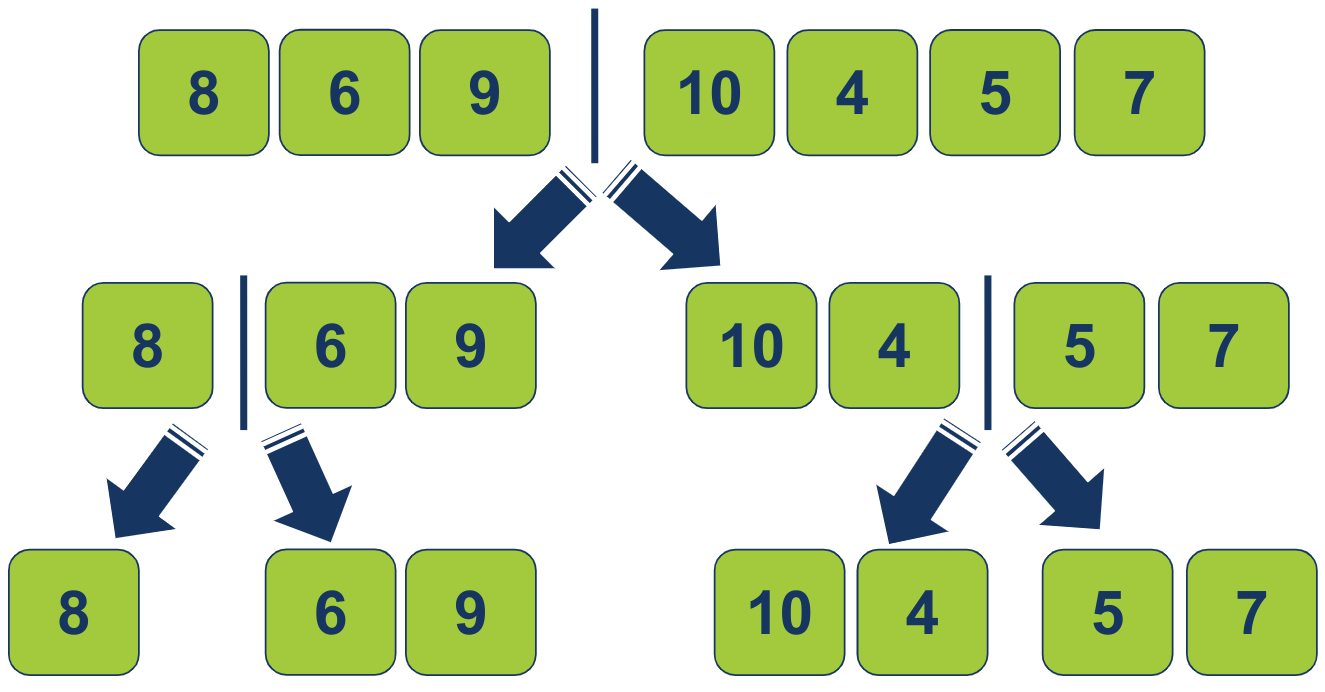
האלגוריתם יחלק שנית את 2 תת הרשימות ל-4 תת רשימות:

החלוקה האחרונה היא כאשר האלגוריתם יחלק את 4 תת הרשימות ל-7 תת רשימות שכל אחת מהם תכיל פריט 1:

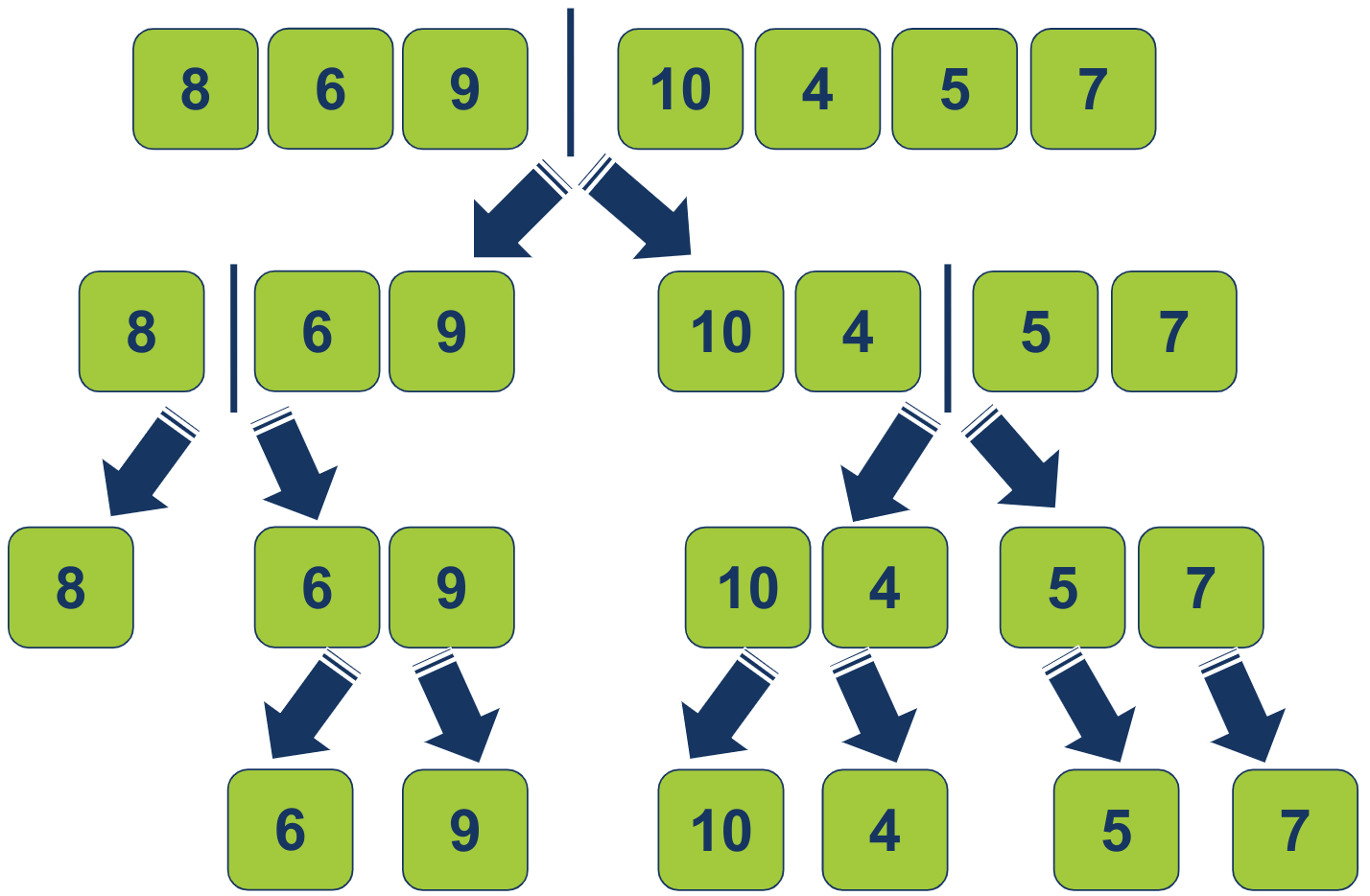
• מספר תת הרשימות בשלב הסופי של החלוקה בהכרח שווה למספר הפריטים ברשימה הגדולה איתה התחלנו את התהליך.

ב. שלב המיזוג

אחרי שהאלגוריתם חילק את הרשימה לתת רשימות בכל אחת מהם פריט 1 מגיע שלב המיזוג בו משווים צמדי רשימות לצורך מיזוגם:

האלגוריתם ימזג 2 רשימות. אחת המכילה 9 ושנייה המכילה 6. 6 קטן מ-9 וזה יהיה הסדר ברשימה הממוזגת:

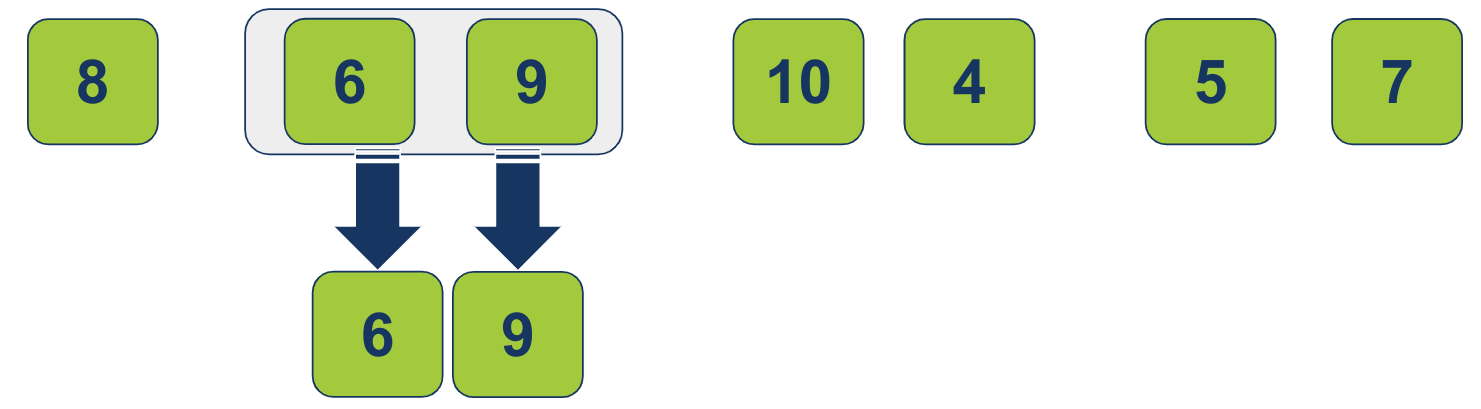
האלגוריתם ימזג 2 רשימות נוספות. אחת המכילה 4 ושנייה המכילה 10. 4 קטן מ-10 וזה יהיה הסדר ברשימה הממוזגת:

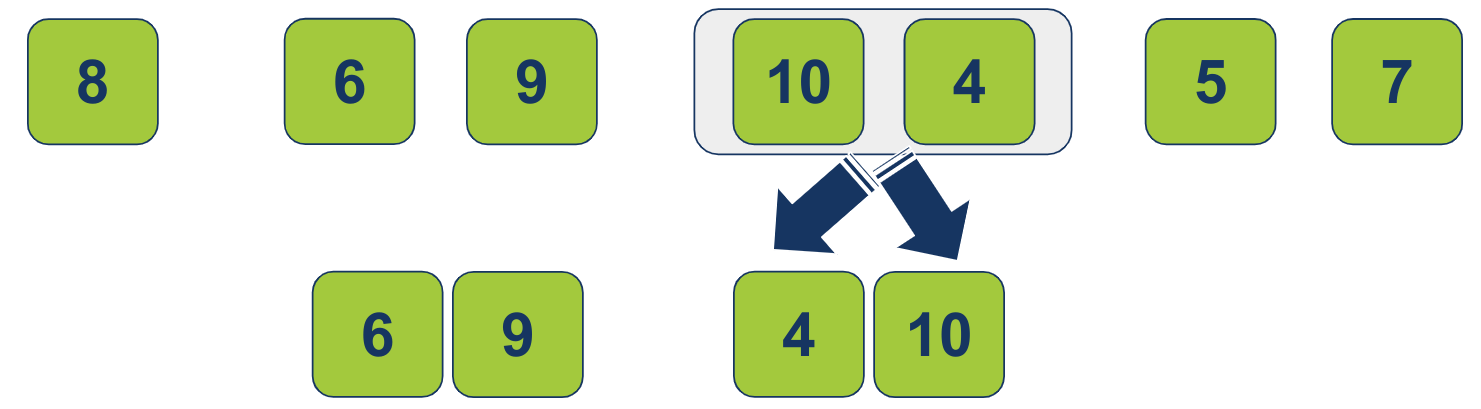
האלגוריתם ימזג 2 רשימות נוספות. אחת המכילה 5 ושנייה המכילה 7. 5 קטן מ-7 וזה יהיה הסדר ברשימה הממוזגת:

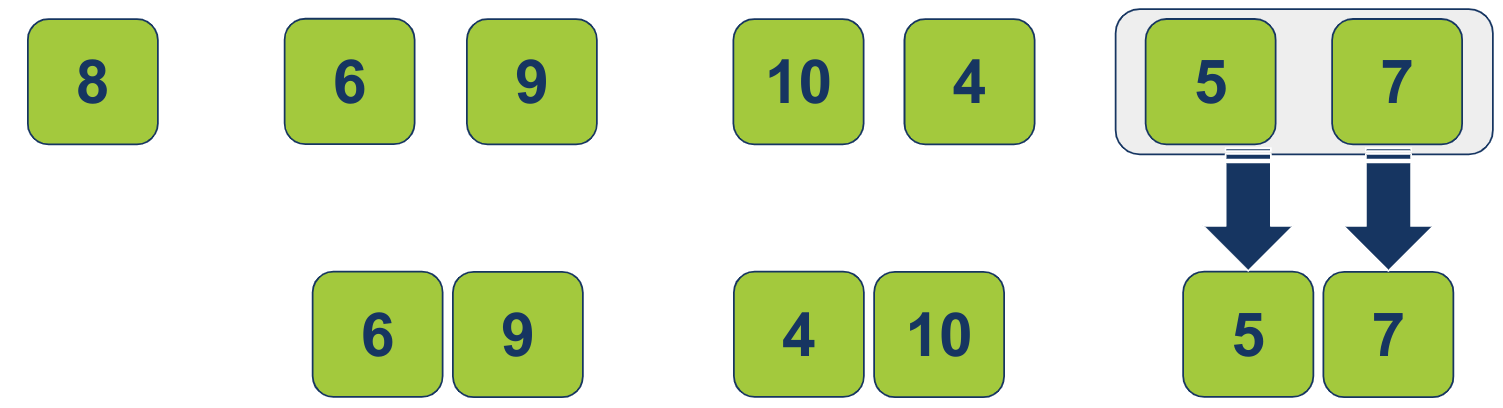
אחרי שהאלגוריתם סיים את השלב של מיזוג רשימות הפריטים הבודדים לרשימות המכילות 2 פריטים ממוינים כל אחת, הוא יעבור למיין ולמזג את הרשימות המכילות 2 פריטים לרשימות המונות 4 פריטים ממוינים כל אחת.

נתחיל ממיזוג הרשימות 8 מימין ו 6-9 משמאל. לשם המיזוג, נפעיל 2 מצביעים, אחד לכל רשימה, הסורקים משמאל לימין, ועל ידי כך עוקבים אחר הפריטים אותם משווים. המצביעים (מסומנים בירוק בתמונה) מורים על הפריטים 8 מהרשימה השמאלית ו-6 מהימנית. כיוון ש-6 הוא הפריט בעל הערך הנמוך יותר הוא יעבור לרשימה הממוזגת:

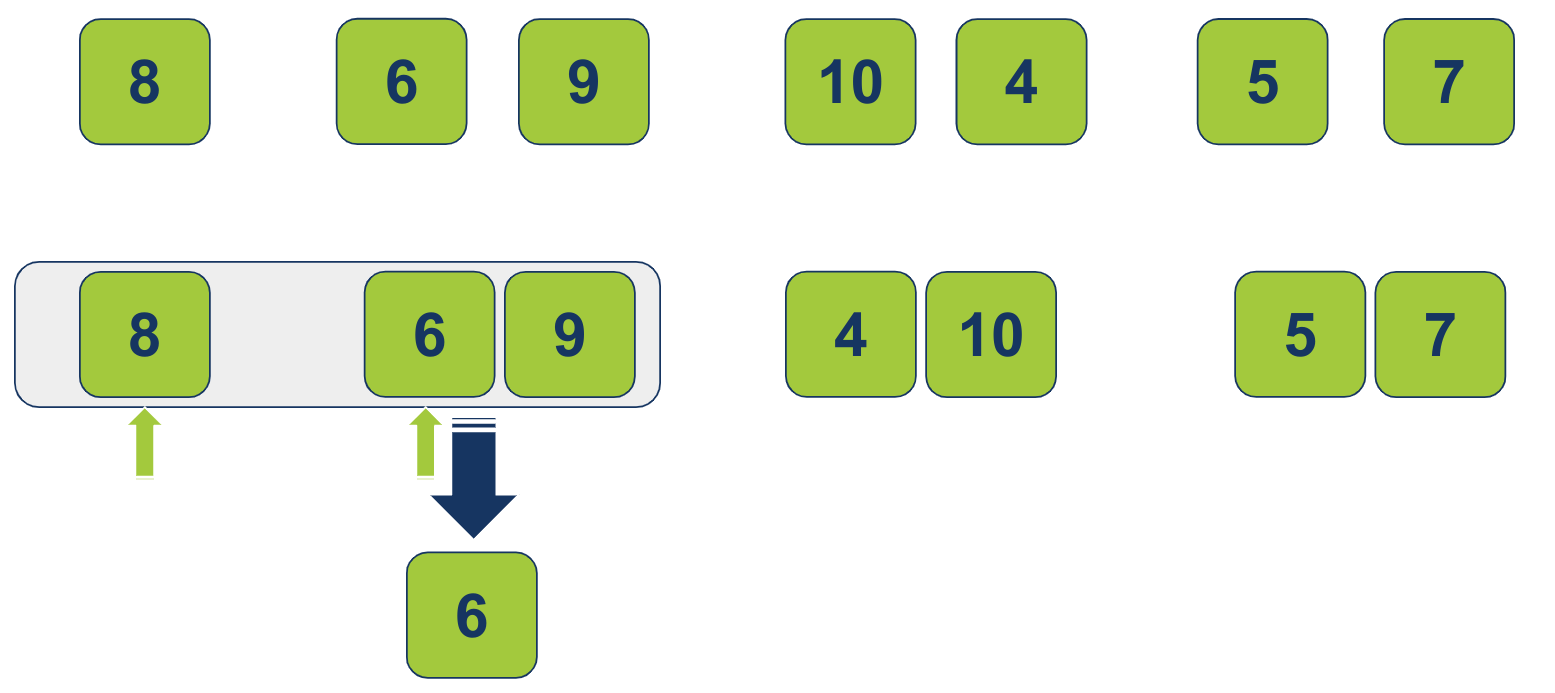
המצביע ימשיך במסעו לימין. בהשוואה בין 8 מהרשימה השמאלית ל-9 מהימנית, הפריט 8 הוא הנמוך יותר, ועל כן יעבור לרשימה הממוזגת:

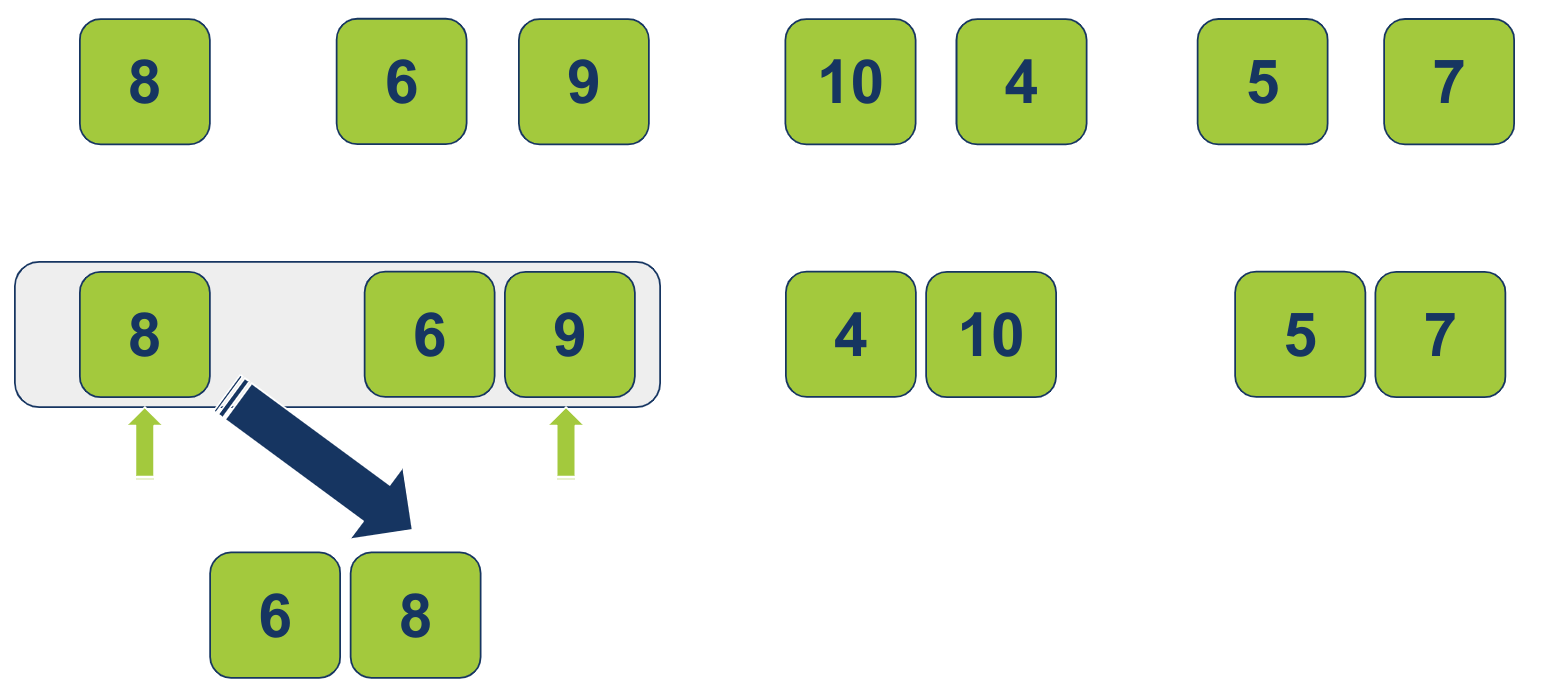
המצביע ברשימה הימנית הגיע לסוף הדרך כי אין לו יותר לאן להתקדם, ולכן סיים את תפקידו. נשארנו רק עם המצביע ברשימה השמאלית. כיוון שהוא מצביע על הפריט 9, נעביר את הפריט לרשימה הממוזגת.

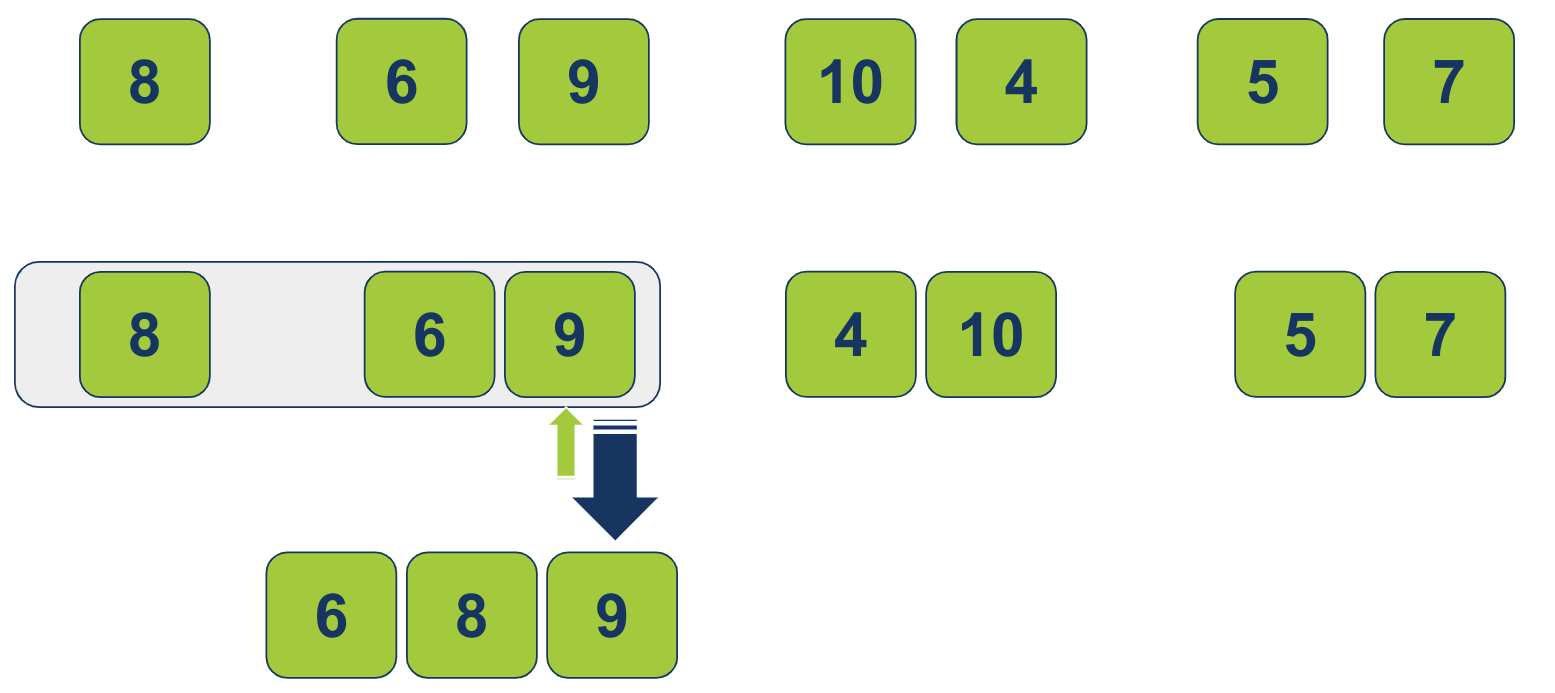
• התחלנו עם 2 רשימות. באחת 2 פריטים. בשנייה פריט 1, מיינו ומיזגנו וכתוצאה מכך קיבלנו רשימה ובה 3 פריטים.

הפונקציה הממזגת תעבור לטפל בשתי תת הרשימות: 4-10 ו 5-7 עליהם יוצבו 2 מצביעים. 1 לכל רשימה. המצביעים יורו על הפריטים שנמצאים בעמדות האינדקס השמאליות. כיוון שהפריט 4 מהרשימה השמאלית קטן יותר מ-5 מהרשימה הימנית, 4 יהפוך להיות הפריט הראשון ברשימה הממוזגת:

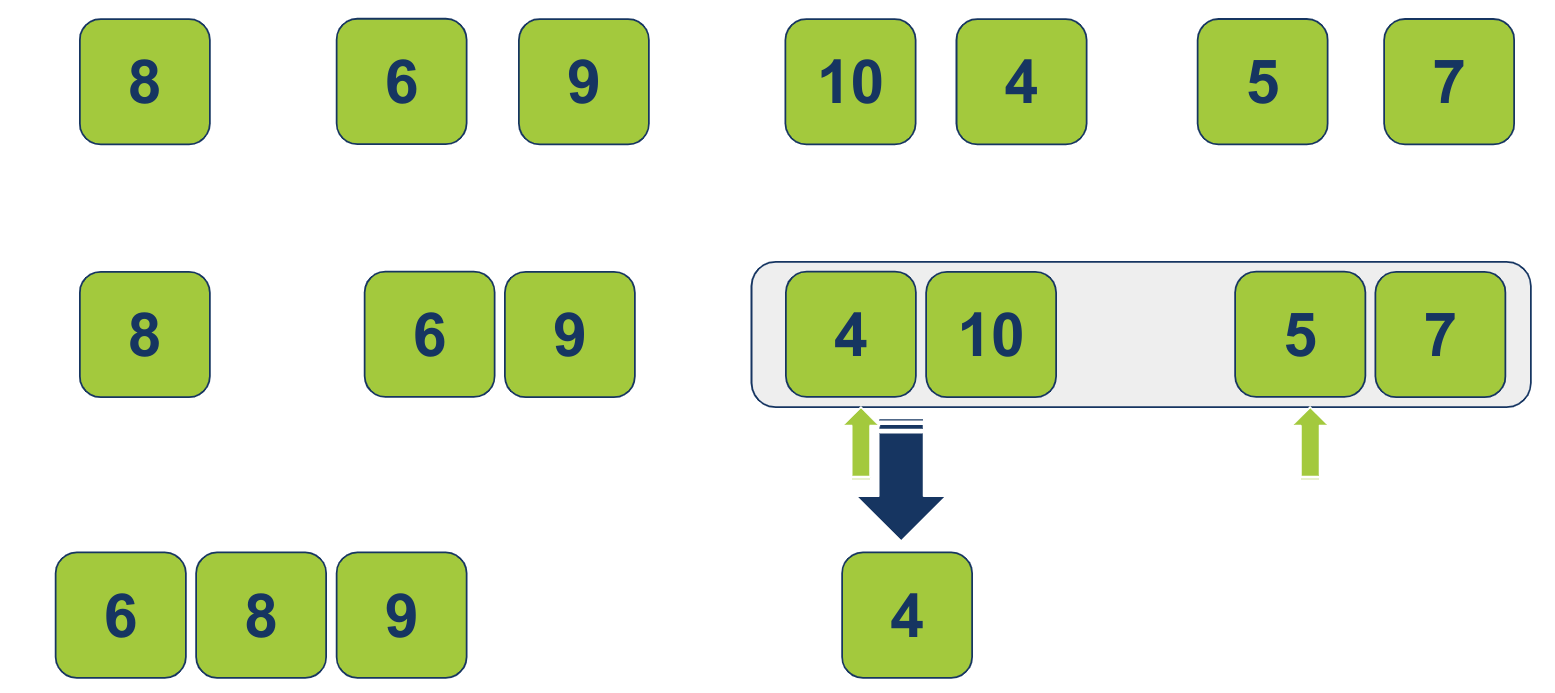
המצביע ברשימה השמאלית יזוז צעד אחד ימינה. עכשיו ההשוואה היא בין הפריט 10 מהרשימה השמאלית לפריט 5 מהרשימה הימנית. כיוון ש-5 הוא הקטן יותר הוא יעבור לרשימה הממוזגת:

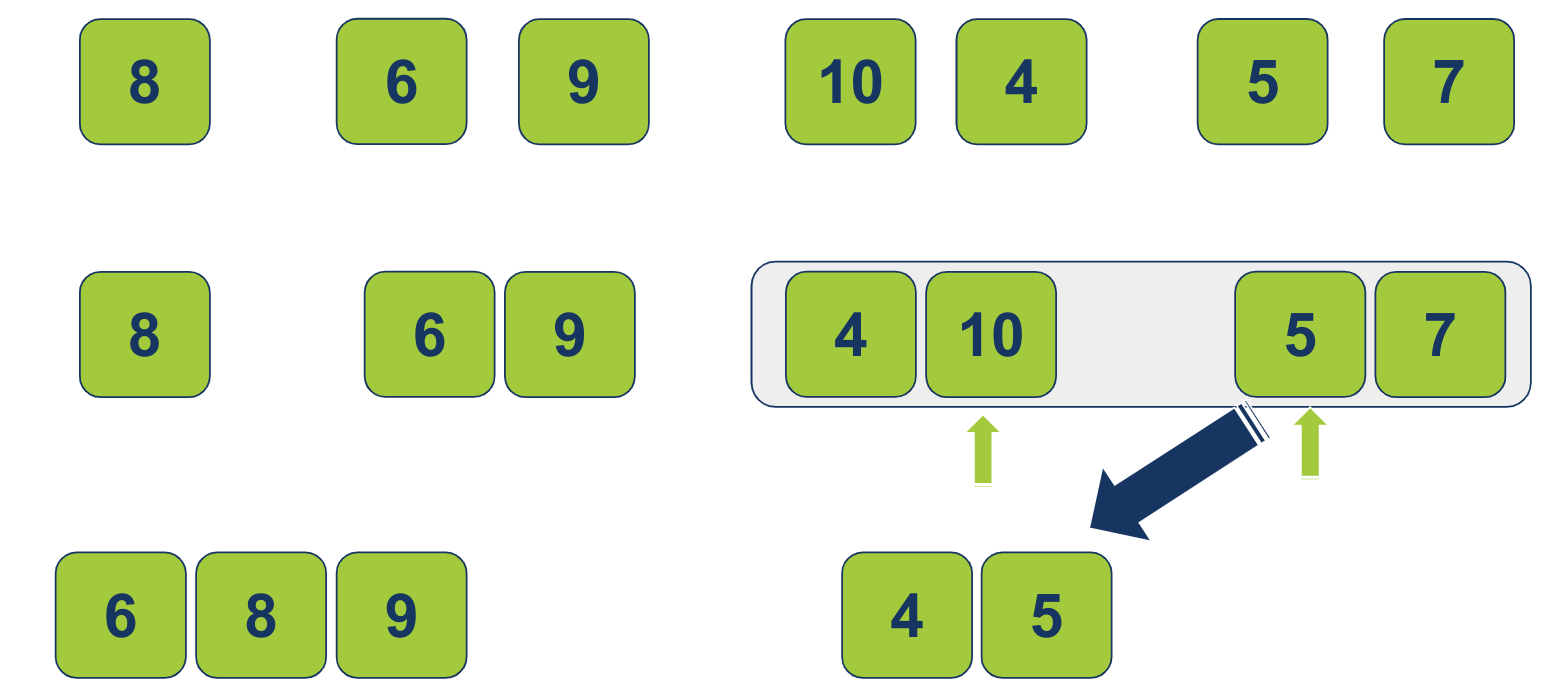
המצביע ברשימה הימנית יזוז צעד אחד ימינה, ועכשיו ההשוואה היא בין 7 מימין ל-10 משמאל. 7 הוא הנמוך יותר ועל כן יעבור לרשימה הממוזגת:

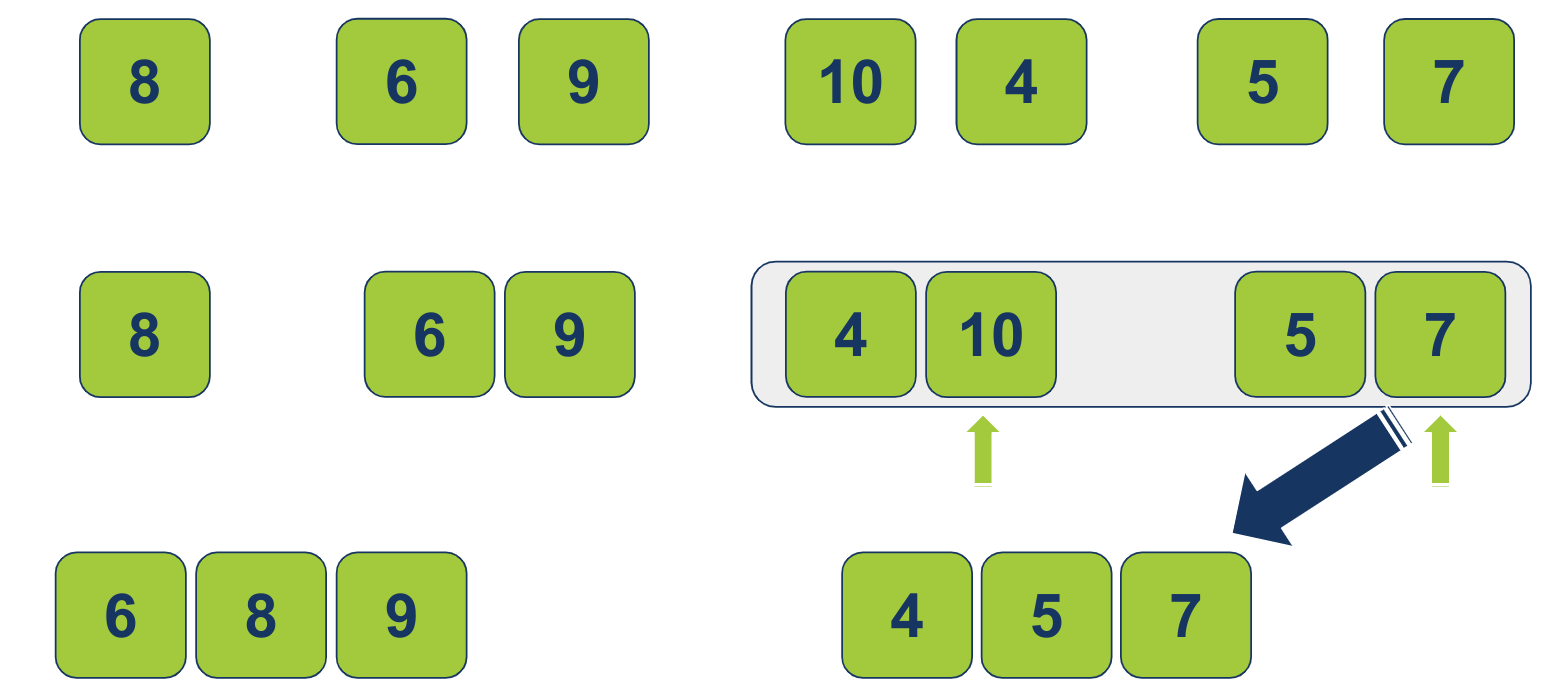
המצביע ברשימה הימנית לא יכול להתקדם יותר ולכן סיים את דרכו. נשאר רק המצביע השמאלי. ניקח את הפריט עליו הוא מורה (10) ונעביר לרשימה הממוזגת:

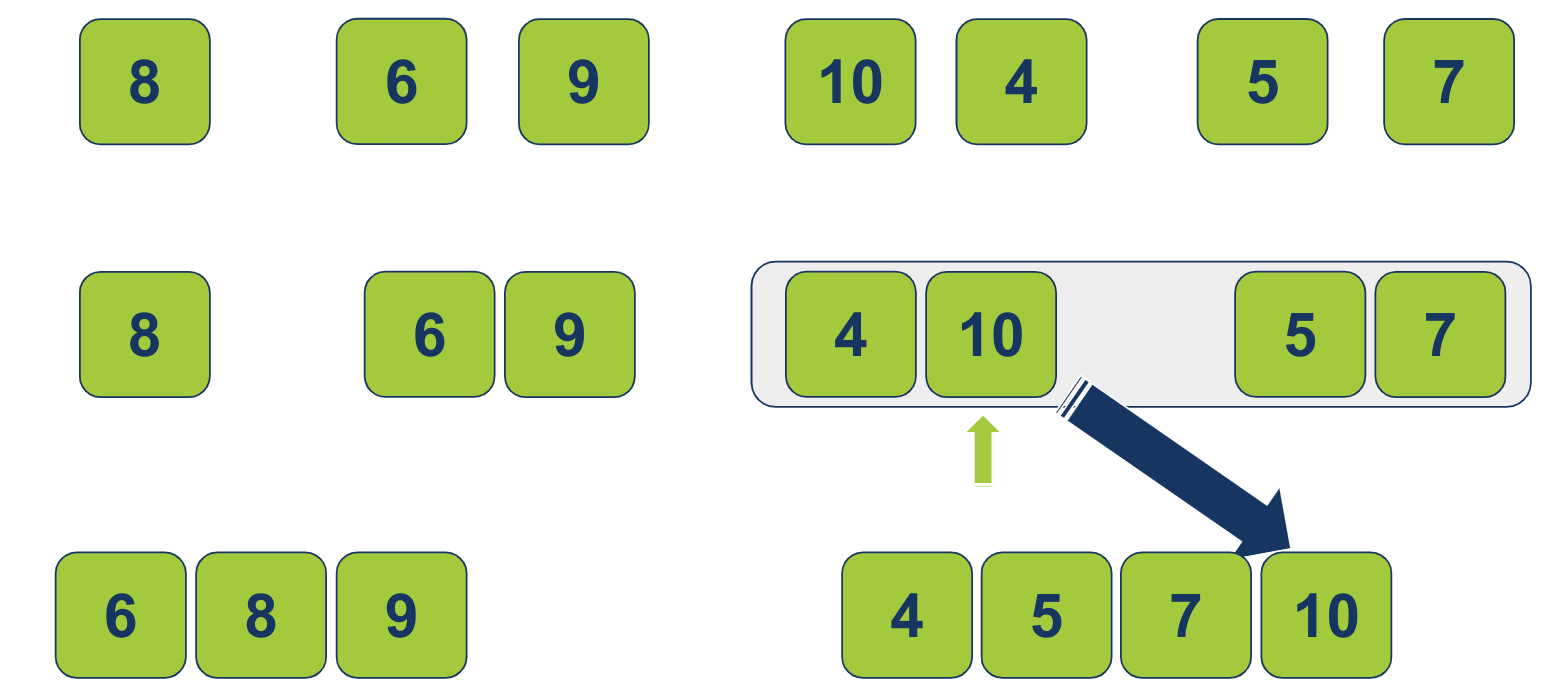
את השלב השני של תהליך המיזוג התחלנו עם 4 רשימות ממוינות וסיימנו עם 2.

את השלב השלישי של תהליך המיזוג יתחיל האלגוריתם עם 2 רשימות ממוינות ויסיים עם 1 גדולה.

נציב מצביע אחד על הפריט הראשון של הרשימה השמאלית (6) ומצביע שני על הפריט הראשון של הרשימה הימנית (4). נשווה ביניהם, ונוסיף לרשימה הממוינת את הקטן מביניהם (4):

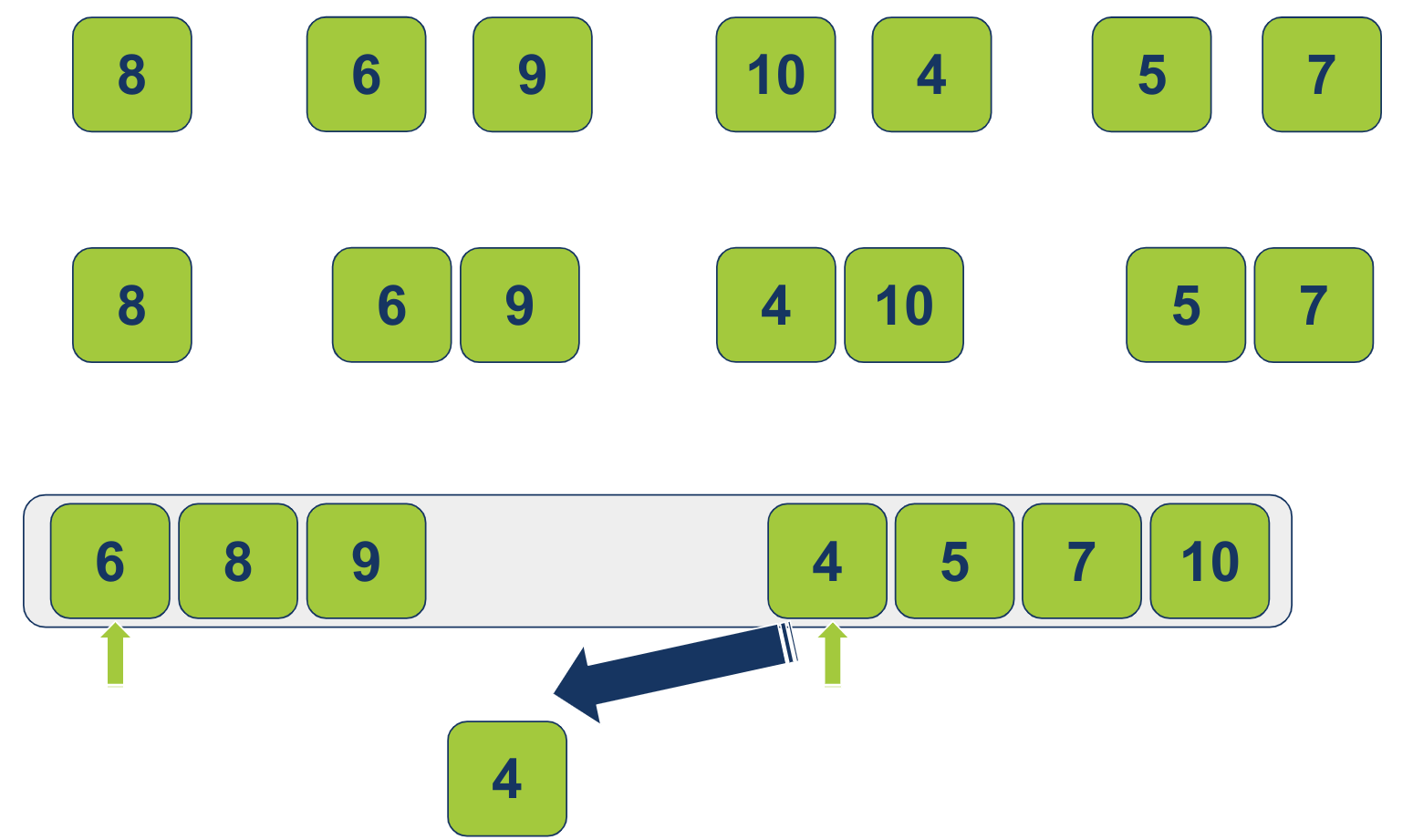
כיוון שהקטן הגיע מהרשימה הימנית, נזיז את המצביע הימני עמדה 1 ימינה. עכשיו ההשוואה היא בין 5 מימין ל-6 משמאל. 5 נמוך יותר. על כן יעבור לרשימה הממוינת:

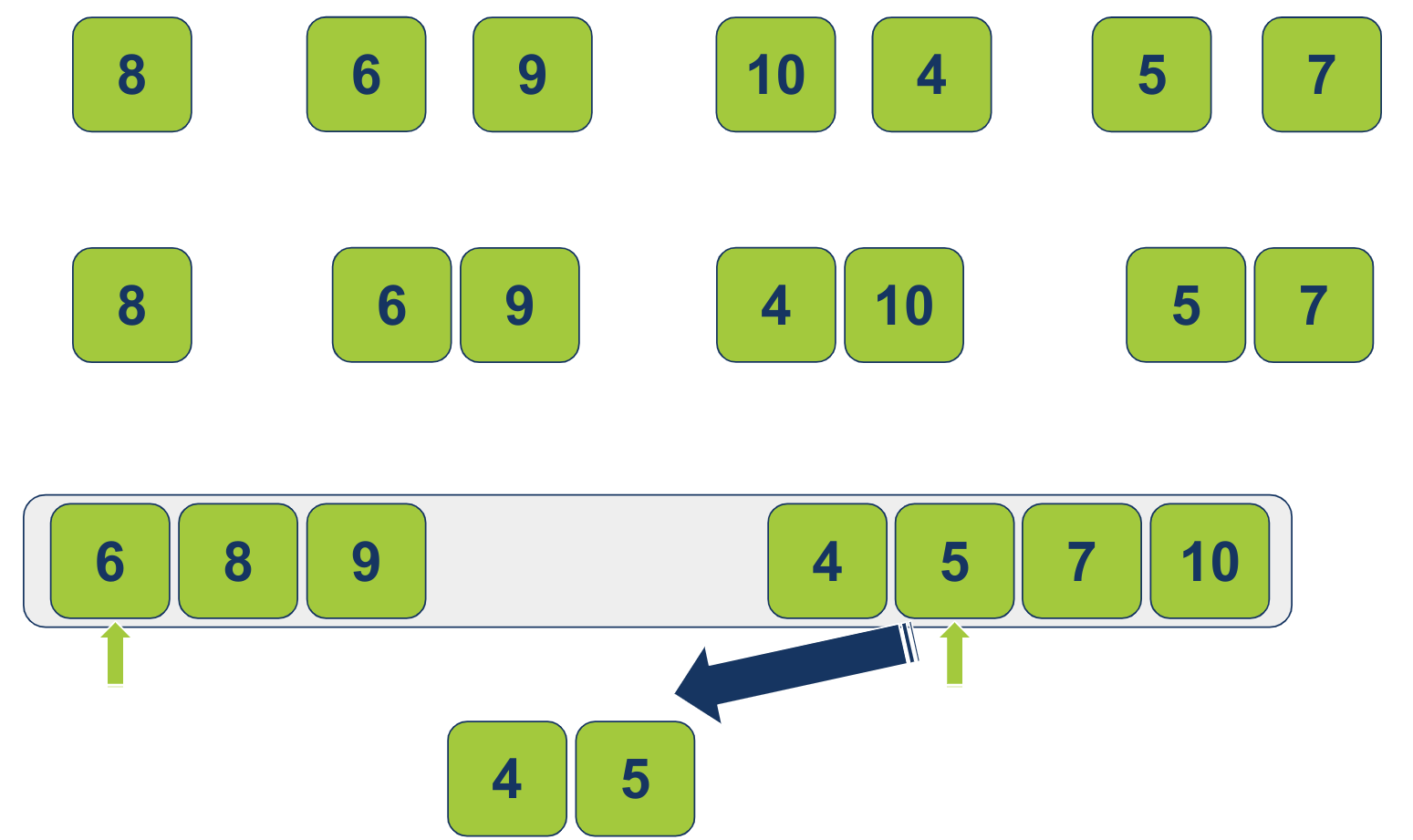
כיוון שהקטן הגיע מהרשימה הימנית, נזיז את המצביע הימני עמדה 1 ימינה. עכשיו ההשוואה היא בין 7 מימין ל-6 משמאל. 6 נמוך יותר. על כן יעבור לרשימה הממוינת:

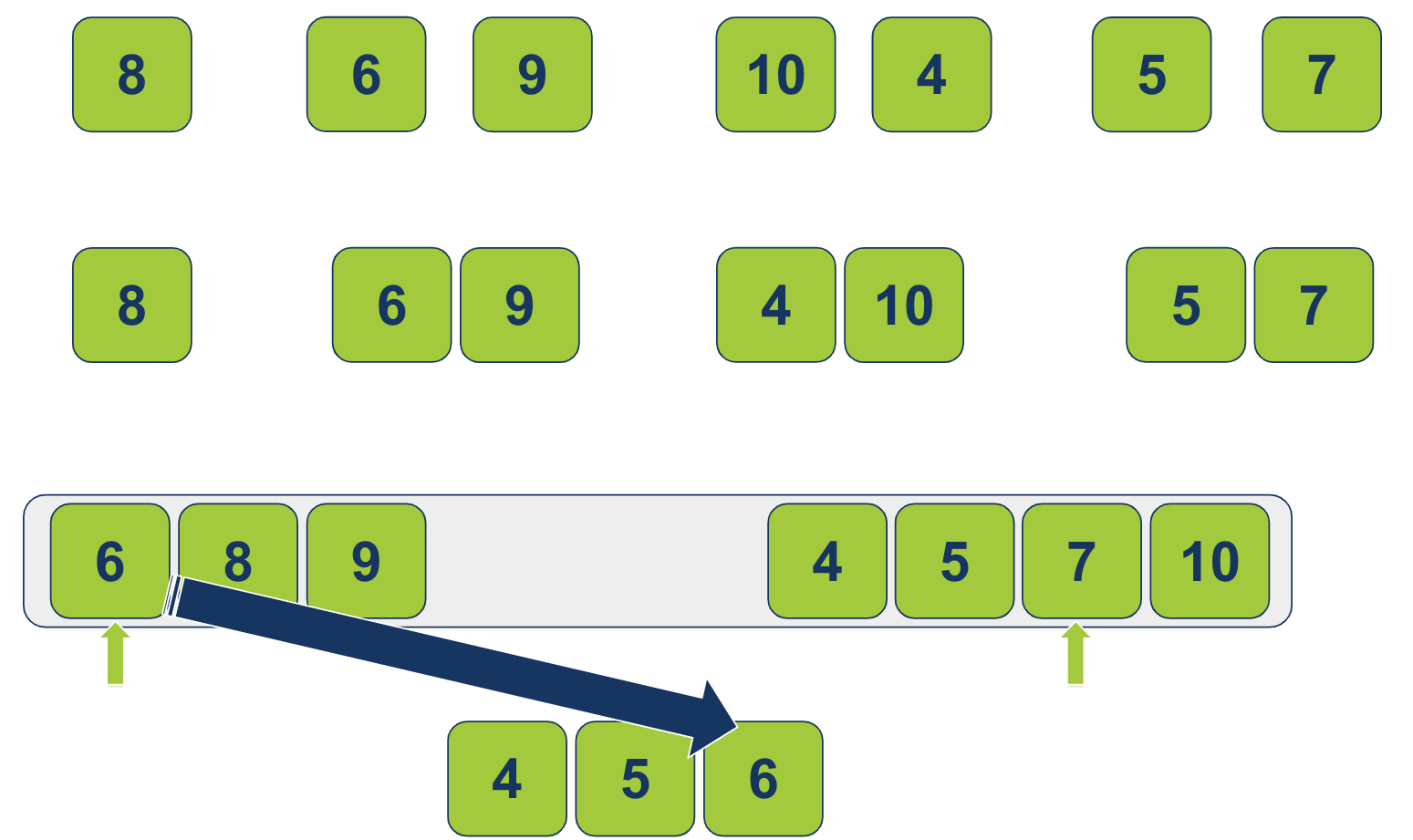
כיוון שהקטן הגיע מהרשימה השמאלית, נזיז את המצביע השמאלי עמדה 1 ימינה. עכשיו ההשוואה היא בין 8 משמאל ל-7 מימין. 7 נמוך יותר. על כן יעבור לרשימה הממוינת:

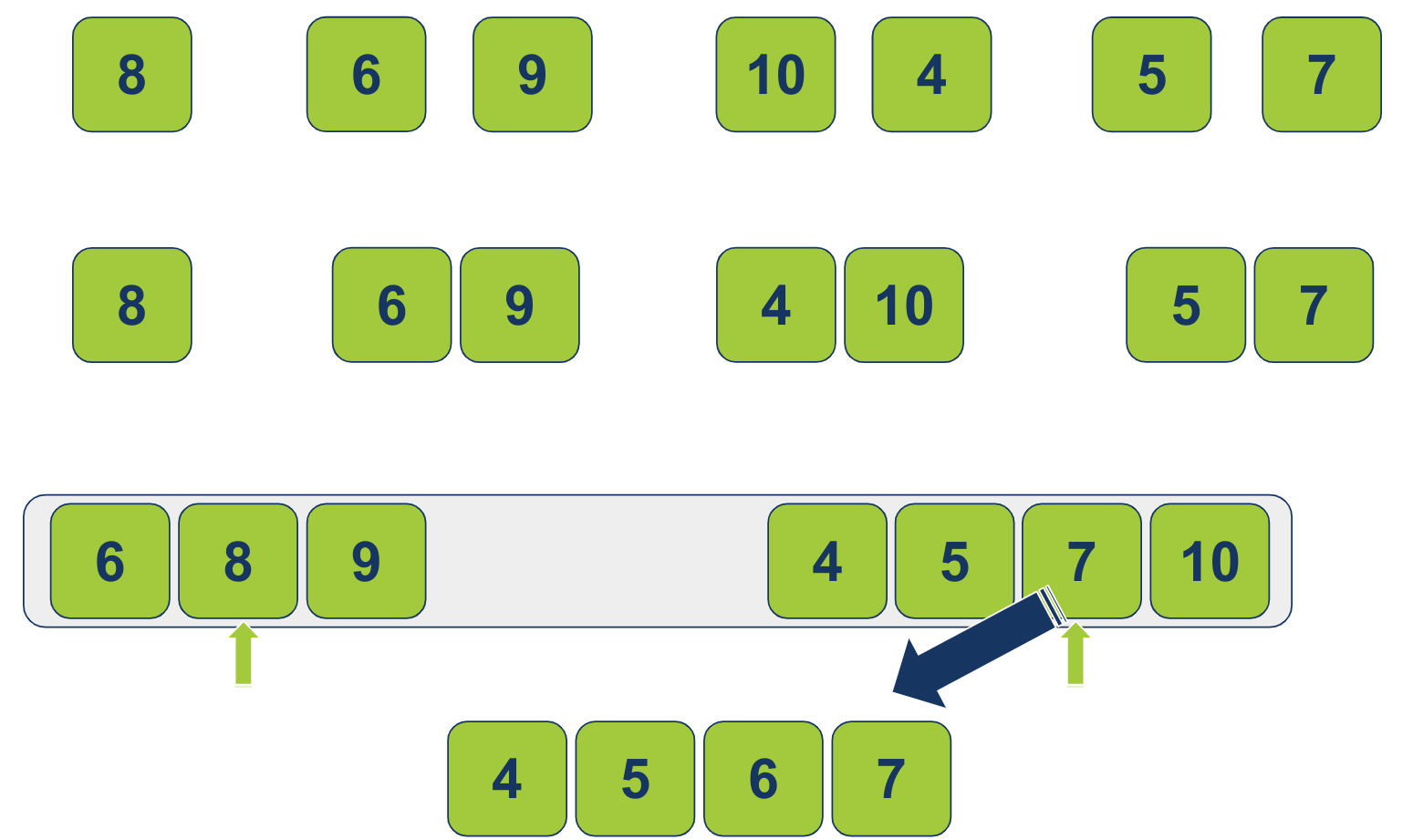
כיוון שהקטן הגיע מהרשימה הימנית, נזיז את המצביע הימני מקום אחד ימינה. הפריט 8 משמאל קטן מ-10 עליו מורה המצביע מימין. נעביר את 8 לרשימה הממוינת:

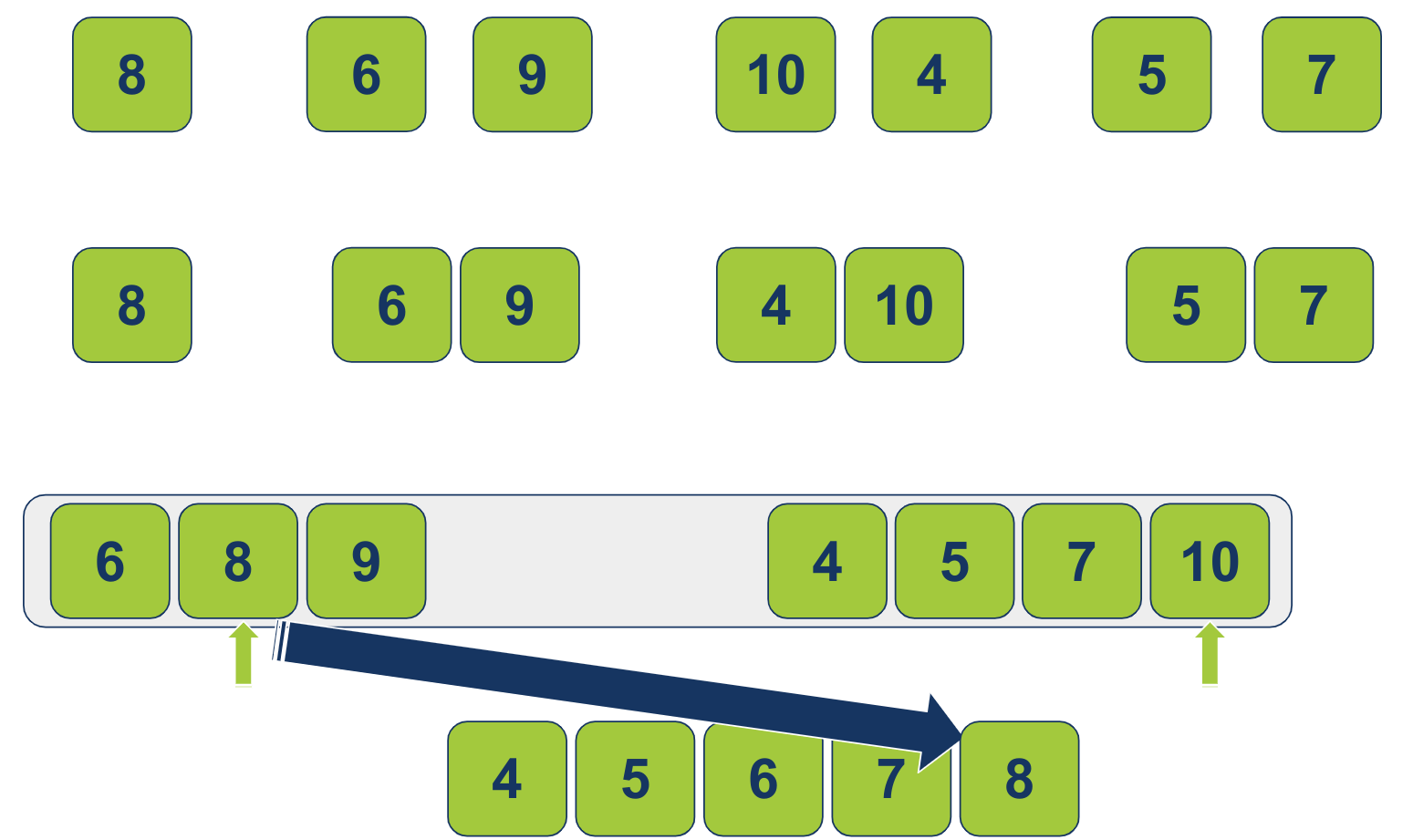
כיוון שהקטן הגיע מהרשימה השמאלית, נזיז את המצביע השמאלי מקום אחד ימינה. הפריט 9 משמאל קטן יותר מ-10 מימין. נעביר את 9 לרשימה הממוינת:

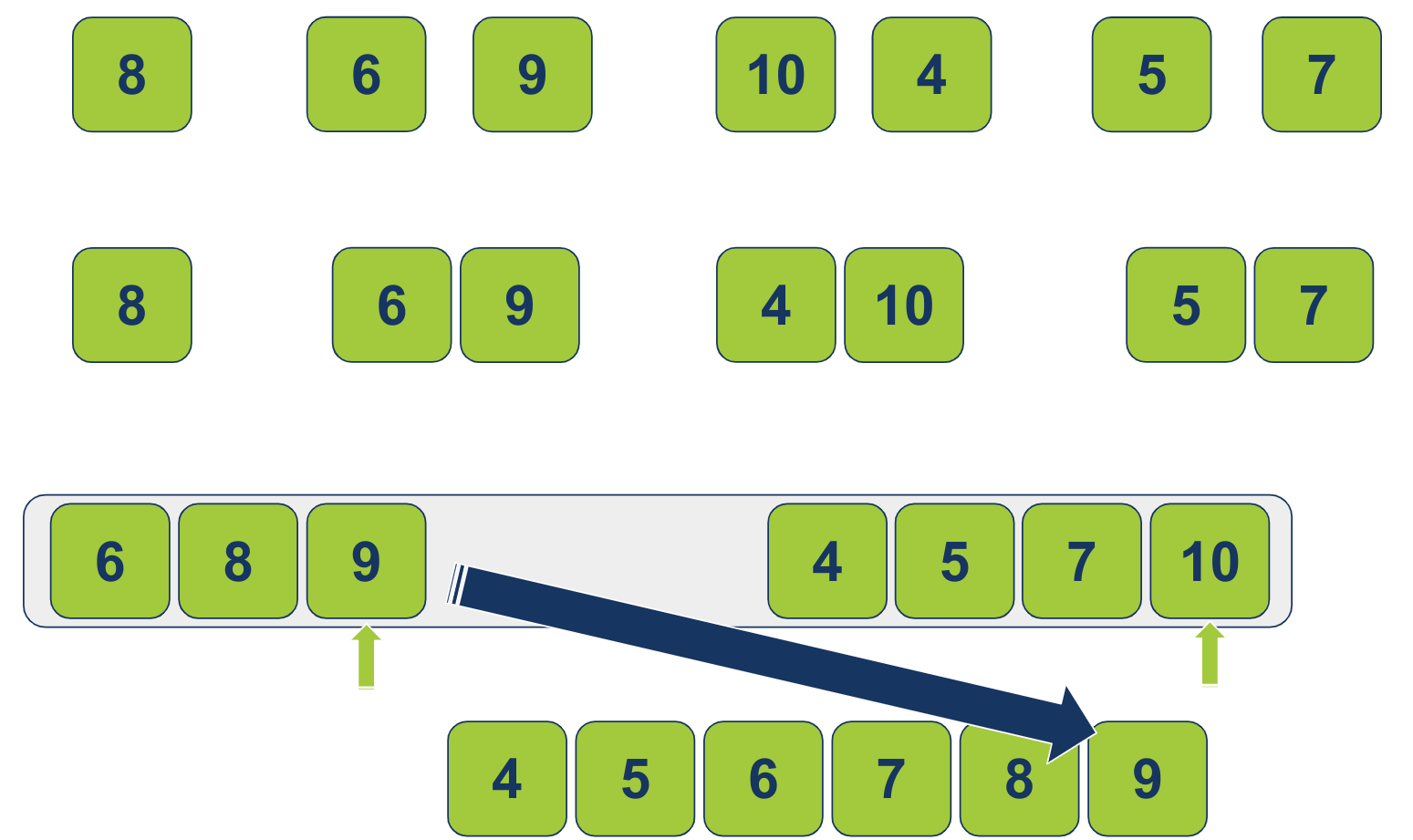
המצביע משמאל לא יכול להתקדם יותר ועל כן יצא משימוש. נשארנו רק עם המצביע מימין. נעביר את הפריט עליו הוא מצביע (10) לרשימה הממוינת:

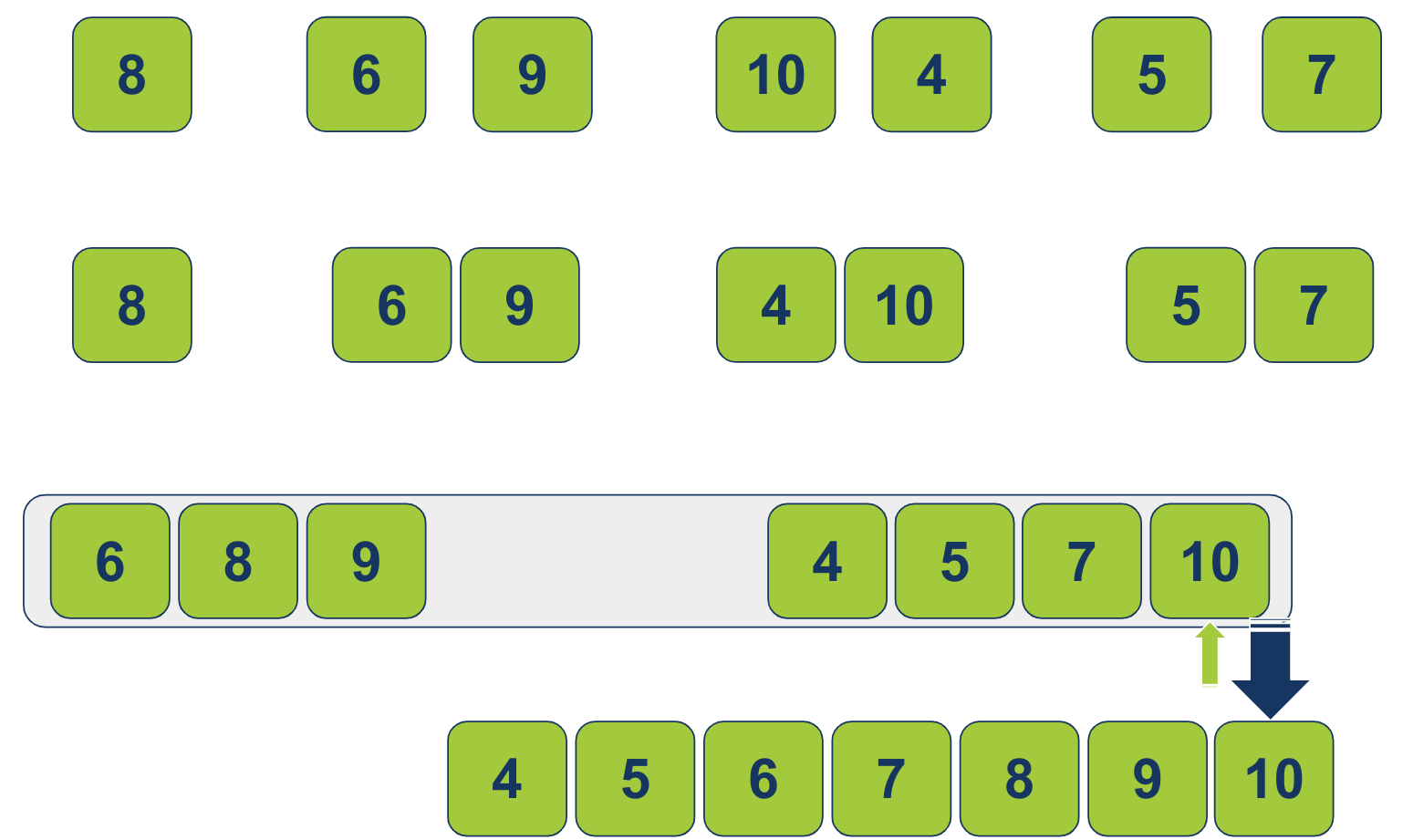
המצביע מימין לא יכול להתקדם יותר. לכן יצא משימוש. נשארנו עם רשימה 1 ממוינת:

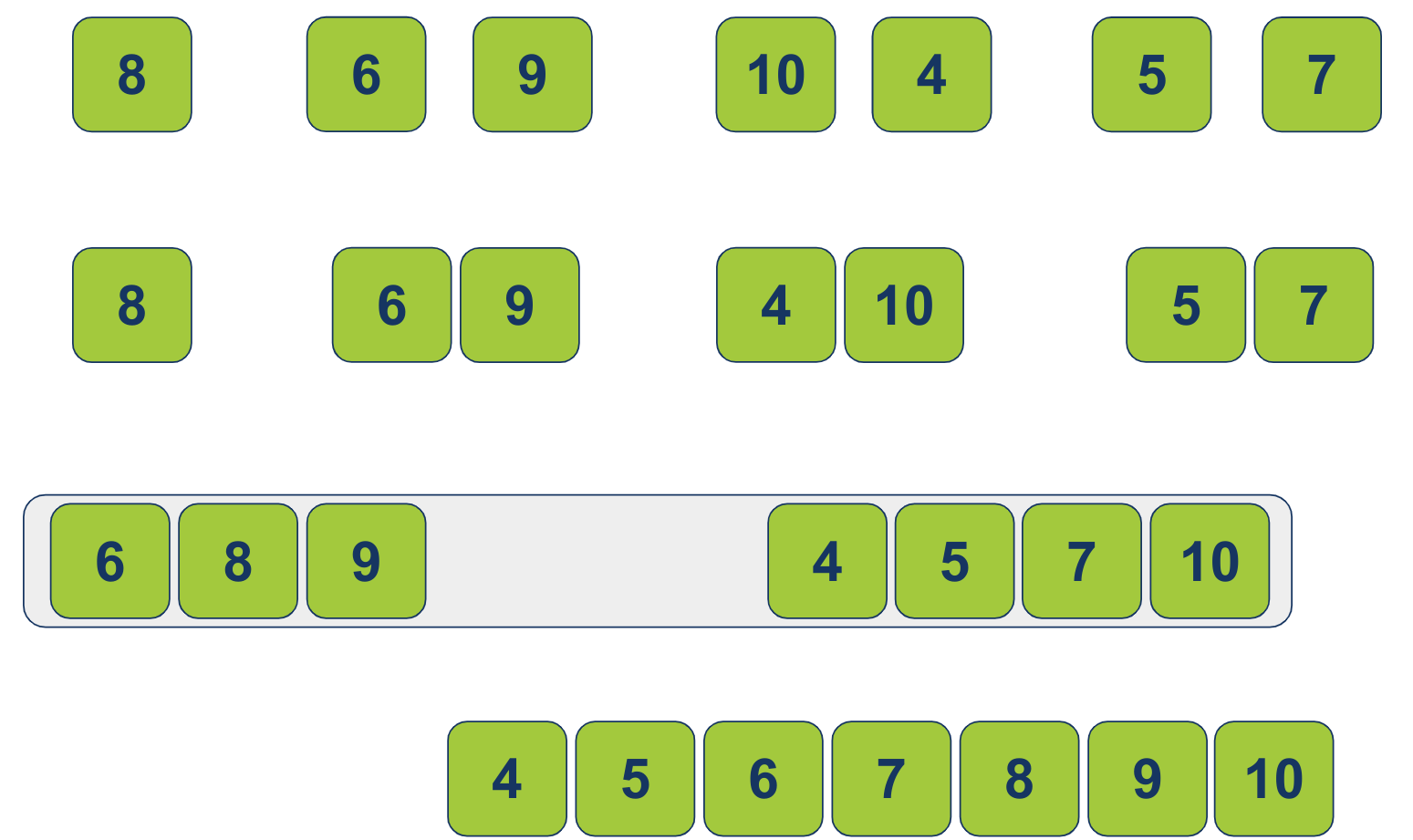
זהו! אלגוריתם מיון מיזוג סיים למיין את הרשימה.

קוד פייתון של מיון מיזוג

הקוד מורכב משלוש פונקציות:

1. sort() - אשר עורכת בדיקה ראשונית של המערך וקוראת ל-split().
2. split() - אשר מפרקת את המערך באופן רקורסיבי לתתי מערכים באורך 1 או 0 פריטים ואז קוראת ל- merge().
3. merge() - אשר מרכיבה את הרשימה לפי הסדר הנכון של הפריטים.

הפונקציה sort() להלן מוודאת שהמערך מכיל לפחות 2 פריטים מה שמאפשר לעבוד על המערך, ואם זה המצב אז קוראת ל-sort(). אחרת מחזירה את המערך כי הוא קצר מכדי שניתן יהיה לעבוד איתו:

def sort(arr):
    # Call the split function
    return split(arr)

• הפונקציה sort() מקבלת רשימה כפרמטר.
• הפונקציה מעבירה את המערך לשלב הפיצול לו אחראית הפונקציה split().

הפונקציה הרקורסיבית split() מקבלת רשימה של פריטים אותם היא צריכה לפרק לרשימות באורך לכל היותר פריט אחד. במקרים הרקורסיביים (בהם הרשימה מכילה לפחות 2 פריטים) הרשימה תפוצל סביב נקודת האמצע לשתי תתי רשימות - ימנית ושמאלית. כל אחת מתת הרשימות תפוצל אף היא באופן רקורסיבי:

def split(arr):
    """Splits the given array into subarrays each with not more then 1 item."""
    # Base case.
    # A list of zero or a single item is sorted, by definition.
    if len(arr) <= 1:
        return arr

    # Recursive case.
    # Split array into 2 equal size sub arrays
    mid = len(arr) // 2
    left_arr = split(arr[:mid])
    right_arr = split(arr[mid:])

    # Merge both sub arrays by calling the merge() function
    return merge(left_arr, right_arr)

אחרי הפיצול הרקורסיבי נכנסת לפעולה הפונקציה הממזגת merge() המקבלת בתור פרמרטים 2 תתי רשימות ממוינות ומחזירה רשימה 1 ממוינת:

def merge(left_arr, right_arr):
    """Merges two sorted arrays into a single sorted array."""
    merged = []

    left_len = len(left_arr)
    right_len = len(right_arr)
    left_idx = right_idx = 0

    # Compare elements from the left and right arrays
    # to find the smaller element and add it to the merged array
    while left_idx < left_len and right_idx < right_len:
        if left_arr[left_idx] < right_arr[right_idx]:
            merged.append(left_arr[left_idx])
            left_idx += 1
        else:
            merged.append(right_arr[right_idx])
            right_idx += 1

    # Add the remaining elements from the arrays
    merged.extend(left_arr[left_idx:])
    merged.extend(right_arr[right_idx:])

    return merged

• הפונקציה הממזגת merge() מקבלת שני תתי מערכים: `left_arr` ו-`right_arr`, אותם היא ממזגת למערך ממוין יחיד.
• הפונקציה מאתחלת מערך `merged` ריק שתפקידו לאחסן את האלמנטים הממויינים.
• הפונקציה מאתחלת שני משתני אינדקס, left_idx ו-right_idx, שעוקבים אחר מיקום המצביע בכל רגע נתון בתתי המערכים left_arr ו-right_arr.
• בתוך לולאת while מושווים פריטים מתתי המערכים השמאלי והימני ונוסף הפריט שערכו נמוך יותר למערך הממוזג. בכל פעם שפריט נוסף למערך מאחד מתתי המערכים, נוסף 1 למשתנה האינדקס של אותו תת מערך.
• לאחר שהלולאה מסיימת לרוץ, עשויים להיות פריטים שנותרו במערך השמאלי או הימני. הקוד משתמש במתודה הפייתונית extend כדי להוסיף את האלמנטים הנותרים ל-merged.
• לבסוף מוחזר merged המכיל רשימה ממוינת המורכבת משילוב תתי המערכים אותם הפונקציה קיבלה.

נבדוק:

numbers = [8, 6, 9, 10, 4, 7, 5]
sorted_numbers = sort(numbers)
print(sorted_numbers)

התוצאה:

[4, 5, 6, 7, 8, 9, 10]

נבחן עוד מספר מקרי קצה:

def test_merge_sort_empty_array():
    assert sort([]) == []
    print("test_merge_sort_empty_array passed")

def test_merge_sort_array_with_one_element():
    assert sort([1]) == [1]
    print("test_merge_sort_array_with_one_element passed")

def test_merge_sort_sorted_array():
    assert sort([1, 2, 3, 4, 5]) == [1, 2, 3, 4, 5]
    print("test_merge_sort_sorted_array passed")

def test_merge_sort_unsorted_array():
    assert sort([100, 3, -5, 6, 1, 2, -8, 4, 3, 4, -100]) == [-100, -8, -5, 1, 2, 3, 3, 4, 4, 6, 100]
    print("test_merge_sort_unsorted_array passed")

def main():
    test_merge_sort_empty_array()
    test_merge_sort_array_with_one_element()
    test_merge_sort_sorted_array()
    test_merge_sort_unsorted_array()

if __name__ == "__main__":
    main()

• אם זה לא ברור נא לקרוא את המדריכים: מה זה __name__ == __main__ בפייתון? ובשביל להבין בדיקות יחידה בדיקות יחידה unit test בפייתון באמצעות pytest

סיבוכיות זמן של מיון מיזוג

את סיבוכיות הזמן של אלגוריתם merge sort קל להבין אם לוקחים בחשבון את שני השלבים: פיצול ומיזוג.

• שלב הפיצול (אותו מבצעת הפונקציה split()) מחלק את מערכי הקלט לשני חצאים תוך שימוש ברקורסיה אשר ממשיכה לרוץ עד שכל תת-מערך מכיל לכל היותר פריט אחד. בכל חלוקה של המערך, גודל הבעיה קטן בערך בחצי, מה שמצריך log(N) רמות רקורסיה כאשר N הוא מספר פריטי המערך. לפיכך, את משך הפיצול נבטא באמצעות O(log N).
• בכל שלב רקורסיבי של פיצול, נעשית קריאה לפונקציה merge() לצורך מיזוג תתי המערכים. הפונקציה הממזגת דורשת סיבוכיות זמן O(N) כיוון שהיא רצה על כל פריטי המערכים (ימני ושמאלי) שהיא מקבלת כקלט.

כיוון שיש log N רמות רקורסיה בפיצול, ומיזוג בכל רמת רקורסיה דורש סיבוכיות זמן לינארית O(N) סה"כ סיבוכיות הזמן היא מכפלה של סיבוכיות הזמן של כל שלב ולפיכך סה"כ סיבוכיות הזמן של הפונקציה "מיון מיזוג" היא O(NlogN).

Time Complexity = O(splitting)×O(merging) = O(logN)×O(N) = O(NlogN)

סיבוכיות זמן O(NlogN) היא יעילה מה שמאפשר מיון של מערכי נתונים גדולים.

לסיכום

לאלגוריתם מיון מיזוג יש סיבוכיות זמן לינאריתמית O(n log n), מה שהופך אותו ליעיל עבור מערכי נתונים גדולים. זהו אלגוריתם מיון יציב, כלומר הוא שומר על הסדר היחסי של אלמנטים בעלי ערכים שווים. עם זאת, הוא דורש מקום נוסף בזיכרון לצורך תהליך המיזוג, מה שיכול להפוך אותו לפחות יעיל בהשוואה לתהליכי מיון אחרים דוגמת quicksort.

מדריכים נוספים בסדרה ללימוד פייתון שעשויים לעניין אותך

האלגוריתם Quicksort ותהליך החלוקה

אלגוריתם Selection Sort מיון בחירה

אלגוריתם חיפוש בינארי - מהבנה ליישום

big-O ביטוי ליעילות הקוד

פייתון מונחה עצמים 1: מחלקות, אובייקטים, תכונות ומתודות

בדיקות יחידה unit test בפייתון באמצעות pytest

לכל המדריכים בסדרה ללימוד פייתון

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים