התפלגות בינומית שלילית עם פייתון

בשקית שמכילה סוכריות טופי בטעמים שונים ידוע ש-30% מהסוכריות הם בטעם קרמל. מה הסיכוי לאכילת 4 סוכריות בטעם קרמל אם אוכלים 10 סוכריות?

זו רק טעימה מבעיות עליהם ניתן לענות באמצעות הסתברות בינומית שלילית.

שאלות עליהם ניתן לענות באמצעות הסתברות בינומית שלילית בד"כ מקיימות את התנאים הבאים:

• תוצאה בינארית: כל ניסיון מוביל לאחת משתי תוצאות אפשריות, המתוייגות לרוב כ"הצלחה" או "כישלון".
• ניסיונות חוזרים: התרחיש דורש סדרה של ניסיונות חוזרים עד אשר מושג מספר ההצלחות הרצוי.
• מספר קבוע וידוע מראש של הצלחות: קיים מספר מטרה מסוים של הצלחות רצויות.
• ניסיונות בלתי תלויים: כל ניסיון הוא בלתי תלוי באחרים וההסתברות להצלחה הינה קבועה. בדוגמה אותה נראה בהמשך המדריך, שחקן הכדורסל לא מתעייף או נעשה יותר טוב כי הוא זורק יותר לסל. זו ההנחה בכל מקרה.
• ספירת הצלחות: השאלה מבקשת לקבוע את מספר הניסיונות הדרושים כדי להשיג מספר קבוע של הצלחות.

פונקציית ההסתברות הבדידה PMF עבור התפלגות בינומית שלילית

אנחנו מעוניינים במספר הכשלונות k המתרחשים לפני מספר ידוע מראש r של הצלחות בסידרה של ניסויי ברנולי בלתי תלויים.

בכל ניסוי, ייתכנו שתי תוצאות: "הצלחה" (עם סיכוי p) או "כשלון" (עם סיכוי 1-p).

$$ P(Success) = p \\ P(Failure) = 1 - p $$

ממשיכים את סדרת הניסויים עד להצלחה שמספרה r. ואנחנו מעוניינים לגלות את ההסתברות לבדיוק k כשלונות לפני ההצלחה שמספרה r.

מספר הכשלונות, k, עשוי להשתנות אבל מספר הניסונות עד להצלחה שמספרה r הינו קבוע (k+r-1). אנחנו צריכים לספור את מספר הדרכים לסדר (r-1) הצלחות בתוך (k+r-1) ניסיונות, מה שנוכל לחשב באמצעות הנוסחה לחישוב קומבינציות:

$$ \binom{k+r-1}{r-1} $$

עבור סידרת ניסויים הכוללת k כשלונות ו (r-1) הצלחות, ההסתברות היא תוצאת המכפלה בין ההסתברויות ל (r-1) הצלחות (עם הסתברות p) בהסתברות ל-k כשלונות (עם הסתברות (1-p)). מה שנותן:

$$ p^{r-1} (1-p)^k $$

נשלב כדי לקבל את פונקצית ההסתברות הבדידה PMF עבור הסתברות בינומית שלילית:

$$ P(X = k) = \binom{k+r-1}{r-1} p^r (1-p)^k $$

• ההנחה היא שהניסויים אינם תלויים לכן אנחנו יכולים להכפיל בין ההסתברויות שלהם.

תכונות נוספות של התפלגות בינומית שלילית

תוחלת ההתפלגות הבינומית השלילית היא גם הממוצע:

$$ E(x) = \mu = \frac{r}{p} $$

• כאשר r הוא מספר ההצלחות ו-p הוא הסיכוי להצלחה בכל ניסוי.

שונות ההתפלגות הבינומית השלילית היא:

$$ \sigma^2 = \frac{r(1 - p)}{p^2} $$

דוגמה לבעיות אותם ניתן לפתור באמצעות התפלגות בינומית שלילית

מה ההסתברות ששחקן כדורסל חובבני יצליח לקלוע 8 פעמים בניסיון ה-20 שלו בהינתן שהסיכוי שלו לקלוע לסל הוא 30%?

אנחנו יכולים להשיב על השאלה באמצעות ההתפלגות הבינומית השלילית בגלל שאנחנו מעוניינים למצוא את התפלגות הניסויים הדרושים לקבלת מספר ידוע של הצלחות (8 קליעות לסל), כאשר לכל ניסוי יש את אותו סיכוי של הצלחה (30%).

נרכז את הנתונים:

מספר ההצלחות r = 8.

מספר הכשלונות:

$$ k = 20 - 8 = 12 $$

ההסתברות להצלחה בכל ניסוי p = 0.3.

נציב את הערכים בנוסחת ה-PMF עבור הסתברות בינומית שלילית:

$$ P(X = k) = \binom{k+r-1}{r-1} p^r (1-p)^k $$

ונקבל:

$$ \begin{aligned} &P(k = 12) \\ &= \binom{12+8-1}{8-1} 0.3^8 (1-0.3)^{12} \\ &= \binom{19}{7} 0.3^8 0.7^{12} \\ &= 50338 \times 0.00006561 \times 0.0138412872 \\ &= 0.04571 \\ &= 4.571\% \end{aligned} $$

• הסיכוי של שחקן הכדורסל להצליח לקלוע 8 פעמים בזריקה שמספרה 20 בהנתן אחוזי קליעה של 30% הינו 4.571%

כדי לאושש את התוצאה נשתמש בפונקציה scipy.stats.nbinom.pmf() שהיא חלק מספריית scipy של שפת התכנות פייתון.

הפונקציה מקבלת את הפרמטרים:

nbinom.pmf(k, n, p)

• k - מספר הכשלונות.
• n - מספר ההצלחות.
• p - ההסתברות להצלחה בניסוי בודד.

נשתמש בפונקציה כדי לחשב:

import scipy.stats as stats

def basketball_probability(successes, attempts, success_rate):
    failures = attempts - successes
    probability = stats.nbinom.pmf(failures, successes, success_rate)
    return probability * 100  # Convert to percentage

# Example usage
successes = 8
attempts = 20
success_rate = 0.3

probability = basketball_probability(successes, attempts, success_rate)
print(f"The probability of making {successes} successful shots in {attempts} attempts is approximately {probability:.3f}%")

התוצאה:

The probability of making 8 successful shots in 20 attempts is approximately 4.576%

נעזר בפייתון לצורך שרטוט גרף עמודות PMF שיציג לנו את ההסתברות ל-8 הצלחות (כאשר ההסתברות p להצלחה בניסוי בודד הינה 0.3) מתוך מספר x של ניסיונות:

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

def plot_negative_binomial(successes, success_rate, max_attempts):
    x = np.arange(0, max_attempts + 1)  # Range of attempts
    pmf = stats.nbinom.pmf(x - successes, successes, success_rate)

    plt.figure(figsize=(10, 6))
    plt.bar(x, pmf, color='#5fad0d', edgecolor='#5fad0d', width=0.2)
    plt.title('Negative Binomial Distribution PMF')
    plt.xlabel('Number of Attempts')
    plt.ylabel('Probability')
    plt.xticks(np.arange(0, max_attempts + 1, step=2))
    plt.grid(True, linestyle='--', alpha=0.7)

    plt.show()

# Example usage
successes = 8
success_rate = 0.3
max_attempts = 60

plot_negative_binomial(successes, success_rate, max_attempts)

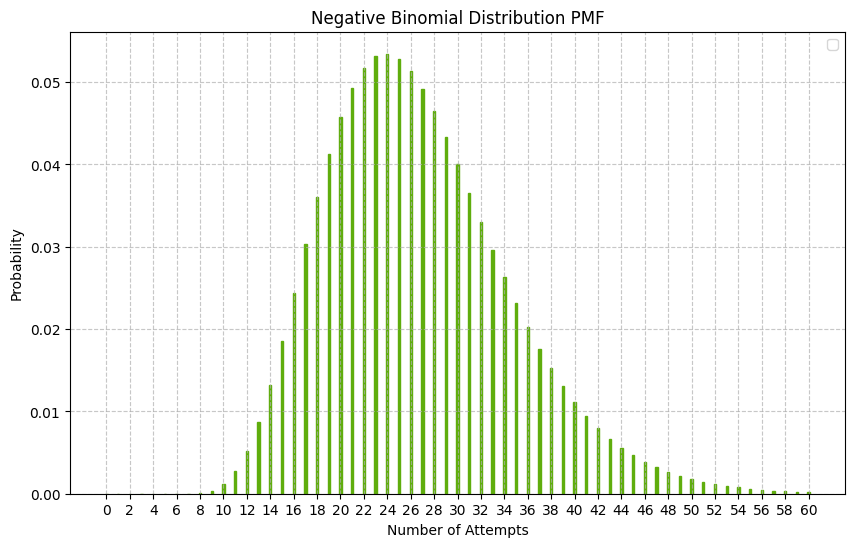
• ציר ה-x מציין את מספר הניסיונות כשבעקרון מספר זה יכול להגיע עד אינסוף אך אינו יכול לרדת לפחות ממספר ההצלחות (במקרה זה 8).
• ציר ה-y מציין את הסיכוי למספר ההצלחות הרצוי (8 במקרה שלנו) מתוך x ניסיונות.

נדגיש על גבי הגרף את העמודה המייצגת 20 ניסיונות:

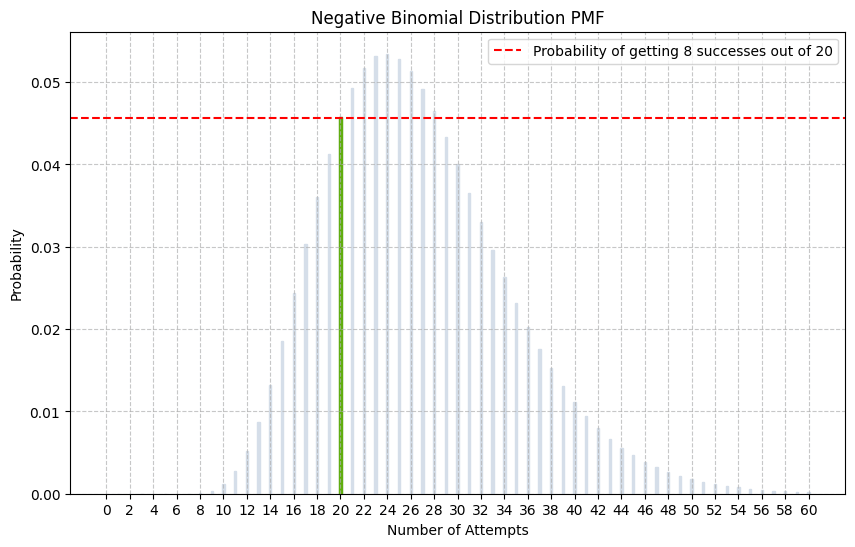
• הגרף גם הוא מאושש את התוצאה שקיבלנו של סיכוי של 4.6% ל-8 הצלחות מתוך 20 ניסיונות כאשר הסיכוי להצלחה הינו 30%.

נעזר בהתפלגות הבינומית לצורך מציאת הממוצע והשונות של מספר הניסיונות הדרושים ל-8 הצלחות כאשר הסיכוי להצלחה בכל ניסוי יחיד הינו 30%.

נחשב את הממוצע:

$$ E(x) = \mu = \frac{r}{p} = \frac{8}{0.3} = 26.7 $$

נחשב את השונות:

$$ \sigma^2 = \frac{r(1 - p)}{p^2} = \frac{8 \times 0.7}{0.3^2} = 62.2 $$

• נדרשים בממוצע כ-26.7 ניסיונות עם שונות של כ-62.2 להשגת 8 הצלחות.

עוד שאלה מעניינת עליה ניתן לענות באמצעות ההתפלגות הבינומית השלילית היא מה ההסתברות לקבל r הצלחות עבור x ניסיונות או פחות.

לדוגמה, מאמן דורש מחניך שלו להמשיך להתאמן עד שהוא קולע 8 סלים. מה הסיכוי של החניך לסיים את האימון תוך 20 זריקות או פחות בהנחה ששיעור הקליעה הינו 30%?

בשביל לחשב את הסיכוי להגיע ל-8 הצלחות ב-20 זריקות או פחות אפשר לסכום את ההסתברויות עבור: 8 מתוך 8 נסיונות, 8 מתוך 9 נסיונות, 8 מתוך 10 נסיונות, וכיו"ב עד 8 מתוך 20. קל לחשב את סכום ההסתברויות באמצעות קוד פייתון ולולאה שרצה ממספר ההצלחות המבוקש ועד למספר הניסיונות וסוכמת:

import scipy.stats as stats

def probability_8_successes_20_trials_or_less(successes, success_rate, max_attempts):
    probability = sum(stats.nbinom.pmf(i - successes, successes, success_rate) for i in range(1, max_attempts + 1))
    return probability

# Example usage
successes = 8
success_rate = 0.3
max_attempts = 20

probability = probability_8_successes_20_trials_or_less(successes, success_rate, max_attempts) * 100
print(f"The probability of getting exactly 8 successes with 20 trials or less is approximately {probability:.2f}%")

התוצאה:

The probability of getting exactly 8 successes with 20 trials or less is approximately 22.77%

נגיע לאותה התוצאה באמצעות הפונקצייה stats.nbinom.cdf(k, n, p) שמקבלת את הפרמטרים: k מספר הכשלונות, n מספר ההצלחות ו- p שיעור ההצלחה בניסוי בודד.

import scipy.stats as stats

def negative_binomial_cdf(successes, attempts, success_rate):
    failures = attempts - successes
    cdf = stats.nbinom.cdf(failures, successes, success_rate)
    return cdf * 100  # Convert to percentage

# Example usage
successes = 8
attempts = 20
success_rate = 0.3

cdf_value = negative_binomial_cdf(successes, attempts, success_rate)
print(f"The probability of getting exactly 8 successes with 20 trials or less is approximately {cdf_value:.2f}%")

התוצאה:

The probability of getting exactly 8 successes with 20 trials or less is approximately 22.77%

• פונקצית ההתפלגות המצטברת CDF מחשבת את ההסתברות לקבל ערך קטן או שווה ל-x. במקרה של התפלגות בדידה, דוגמת הבינומית השלילית, ערך ה-CDF עבור משתנה x שווה לסכום ההסתברויות עד ל-x כולל.

ראינו כיצד לחשב את ההסתברות לקיום 8 הצלחות בפחות מ-20 ניסיונות, אך מה בנוגע להסתברות לקיום 8 הצלחות ביותר מ-20 ניסיונות?

כדי לחשב את ההסתברות לקיום 8 הצלחות ביותר מ-20 ניסיונות, עלינו לשים לב שסכום כל ההסתברויות צריך להיות שווה ל-1 (כאשר סוכמים את ההסתברויות ל-8 קליעות מתוך 8 ניסיונות, 8 מתוך 9, 8 מתוך 10, וכן הלאה, עד ל-8 מתוך 20). לכן, עלינו להפחית את ההסתברויות המצטברות עד ל-20 מתוך 1. לדוגמה, במקרה שלנו:

$$ P(x > 20) = 1 - P(x \leq 20) = 1 - 0.2277 = 0.7723 = 77.23\% $$

• ההסתברות שהחניך יצליח לקלוע 8 סלים ביותר מ-20 ניסיונות היא 77.23%

מקרי שימוש נוספים להתפלגות בינומית שלילית

להלן כמה תחומים בהם ניתן להשתמש בהתפלגות בינומית שלילית:

בספורט: ניתן להשתמש בהתפלגות הבינומית השלילית כדי לחזות את מספר המשחקים שקבוצה צריכה לשחק כדי להשיג מספר מסוים של ניצחונות, בהינתן הסתברות קבועה לניצחון בכל משחק. לדוגמה, בכדורגל, אפשר להעריך את מספר המשחקים שקבוצה צריכה לנצח בהם כדי להבטיח מקום בפלייאוף.

ביטוח: בתחום הביטוח, ניתן להשתמש בהתפלגות הבינומית השלילית כדי לתאר את מספר תביעות הביטוח שהוגשו עד שאושר מספר מסוים של תביעות. זה עוזר לחברות ביטוח להעריך סיכונים ולקבוע עתודות מתאימות לתשלומי תביעות.

שיווק ומכירות ניתן להשתמש בהתפלגות הבינומית השלילית לצורך ניתוח של מספר האינטראקציות עם לקוחות (כגון ביקורים באתר, מיילים שנשלחו או שיחות טלפון שבוצעו) עד להתרחשות מספר מסוים של רכישות. זה עוזר לעסקים להבין את שיעורי ההמרה ולמטב את אסטרטגיות השיווק שלהם.

אקולוגיה: חוקרים משתמשים בהתפלגות הבינומית השלילית כדי לספור ציפורים עד לצפייה במספר מוגדר מראש של מין היעד. הם עושים זאת כדי להעריך את בריאות האוכלוסייה ולנטר תנודות במספר הציפורים, וכך לספק תובנות קריטיות למאמצי שימור וניהול חיות בר.

ייצור: ניתן להשתמש בהתפלגות הבינומית השלילית כדי להעריך את מספר המוצרים הפגומים המיוצרים עד שמאתרים מספר מסוים של פגמים במהלך בדיקות בקרת איכות. זה עוזר ליצרנים להעריך את איכות הייצור ולזהות תחומים הדורשים שיפור.

הסתברויות אחרות דומות לבינומית שלילית

ההתפלגות הגיאומטרית מאפשרת לחשב כמה ניסיונות בלתי תלויים דרושים לקבלת הצלחה ראשונה.

ההתפלגות הבינומית שלילית היא המקרה הכללי של התפלגות גיאומטרית. היא מאפשרת לחשב כמה ניסיונות בלתי תלויים דרושים לקבלת x הצלחות.

ההתפלגות הבינומית מחשבת את מספר ההצלחות במספר ידוע של ניסויים. מספר ההצלחות הוא המשתנה המבוקש.

ההתפלגות הבינומית שלילית מחשבת את מספר הניסויים הדרושים למספר ידוע של הצלחות. מספר הניסויים הוא המשתנה המבוקש.

מדריכים נוספים בסדרה על למידת מכונה שעשויים לעניין אותך

התפלגות בינומית - הלכה למעשה

התפלגות גיאומטרית ישר ולעניין עם קוד פייתון

מדריך הסתברות מעריכית (אקספוננציאלית) מהלכה למעשה עם פייתון

מדריך מעשי על התפלגות פואסנית באמצעות קוד פייתון וציפורים נודדות

לכל המדריכים בנושא של למידת מכונה

אהבתם? לא אהבתם? דרגו!

0 הצבעות, ממוצע 0 מתוך 5 כוכבים